
【题目】某校1200名高三年级学生参加了一次数学测验(满分为100分),为了分析这次数学测验的成绩,从这1200人的数学成绩中随机抽出200人的成绩绘制成如下的统计表,请根据表中提供的信息解决下列问题;
(1)求a、b、c的值;
(2)如果从这1200名学生中随机取一人,试估计这名学生该次数学测验及格的概率p(注:60分及60分以上为及格);
(3)试估计这次数学测验的年级平均分.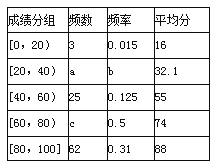
【答案】解:(1)根据频率和为1,得;
b=1﹣(0.015+0.125+0.5+0.31)=0.05,
∴a=200×0.05=10,
c=200×0.5=100;
(2)根据题意,在抽出的200人的数学成绩中,及格的有
100+62=162人,
∴及格率为P=![]() =0.81;
=0.81;
(3)这次数学测验样本的平均分为![]() =
=![]() =73,
=73,
∴这次数学测验的年级平均分大约为73分.
【解析】(1)根据频率和为1,求出b的值,再根据频率、频数与样本容量的关系求出a、c的值;
(2)根据题意,计算及格率P的值;
(3)计算样本数据的平均值![]() 。
。
【考点精析】利用频率分布表对题目进行判断即可得到答案,需要熟知第一步,求极差;第二步,决定组距与组数;第三步,确定分点,将数据分组;第四步,列频率分布表.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:高中数学 来源: 题型:
【题目】【2017南通二模19】已知函数![]() ,
,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数![]() 在x
在x![]() 1处的切线方程;
1处的切线方程;
(2)若存在![]()
![]() ,使得
,使得![]() 成立,其中
成立,其中![]() 为常数,
为常数,
求证:![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
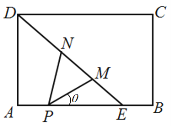
【题目】【2017扬州一模】如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.y=x3 , x∈R
B.y=sinx,x∈R
C.y=﹣x,x∈R
D.y=( ![]() )x , x∈R
)x , x∈R
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017重庆市八中5月模考】已知![]() (
(![]() ),
),![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若在(1)的条件下,当![]() 取最大值时,求证:
取最大值时,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2﹣(a+1)x+1.
(1)若不等式f(x)<mx的解集为{x|1<x<2},求实数a、m的值;
(2)解不等式f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
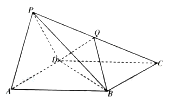
【题目】【2017湖南娄底二模】如图,四棱锥![]() 的底面
的底面![]() 是平行四边形,侧面
是平行四边形,侧面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]()
![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 是棱
是棱![]() 上的点,当
上的点,当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2, ![]() )在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com