已知在等差数列{an}中,a1=120,d=-4,若Sn≤an(n≥2),则n的最小值为( )
A.60
B.62
C.70
D.72
【答案】
分析:由等差数列的首项和公差,表示出前n项的和S
n和通项公式a
n,代入到S
n≤a
n得到关于n的一元二次不等式,求出不等式的解集即可得到n的取值范围,根据n大于等于2得到满足题意的n的范围,根据n的范围即可求出n的最小值.
解答:解:S
n=120n+
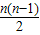
×(-4)=-2n
2+122n,a
n=120-4(n-1)=-4n+124,
因为S
n≤a
n,所以-2n
2+122n≤-4n+124,
化简得:n
2-63n+62≥0即(n-1)(n-62)≥0,
解得:n≥62或n≤1(与n≥2矛盾,舍去)
所以n的最小值为62.
故选B
点评:此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道中档题.

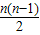 ×(-4)=-2n2+122n,an=120-4(n-1)=-4n+124,
×(-4)=-2n2+122n,an=120-4(n-1)=-4n+124,
