练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图，已知四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且.

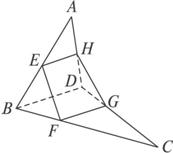
    求证:四边形EFGH是梯形.

    证明：∵E,H分别是AB,AD的中点,

    ∴=,=,==-

    =()==()=(-)

    =()=.

    ∴∥,且||=||≠||.

    ∴四边形EFGH是梯形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：重难点手册　高中数学·必修4（配人教A版新课标） 人教A版新课标 题型：022

    如下图，已知四边形ABCD是矩形，O为对角线AC与BD的交点，设点集M＝{O，A，B，C，D}，向量的集合T＝{|P，Q∈M，且P、Q不重合}，则集合T有________个子集．

    查看答案和解析>>

    科目：高中数学 来源：导学大课堂必修二数学苏教版 苏教版 题型：044

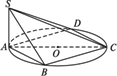
    如下图，已知四边形ABCD内接于半径为R的⊙O，AC为⊙O的直径，点S为平面ABCD所在平面外一点，且SA⊥平面ABCD，∠DAC＝∠ACB＝∠SCA＝30°，求二面角S－CB－A的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，已知正四面体A—BCD中,E、F分别为棱AC、AD的中点,则△BEF在平面ACD上的射影为图中的(正四面体是指所有棱长都相等的空间四边形)（    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，已知曲线C1：y=x3(x≥0)与曲线C2：y=-2x3+3x(x≥0)交于点O、A，直线x=t(0＜t＜1)与曲线C1、C2分别相交于点B、D.

    （1）写出四边形ABOD的面积S与t的函数关系S=f(t);

    （2）讨论f(t)的单调性，并求f(t)的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，已知四边形OADB是以向量=a,=b为边的平行四边形，其中BM=BC，CN=CD.试以向量a,b为一组基底,表示出向量,.

    查看答案和解析>>

    同步练习册答案