练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】等差数列{an}前n项和为Sn ， 已知（a2﹣2）3+2013（a2﹣2）=sin ，（a2013﹣2）3+2013（a2013﹣2）=cos ，则S2014= ．

    【答案】4028
    【解析】解：（a2﹣2）3+2013（a2﹣2）=sin = ，① （a2013﹣2）3+2013（a2013﹣2）=cos =﹣ ，②
    ①+②得，
    （a2﹣2）3+2013（a2﹣2）+（a2013﹣2）3+2013（a2013﹣2）=0，
    即（a2﹣2+a2013﹣2）[（a2﹣2）2﹣（a2﹣2）（a2013﹣2）+（a2013﹣2）2]+2013（a2﹣2+a2013﹣2）=0，
    ∴a2﹣2+a2013﹣2=0，
    即a2+a2013=4，
    ∴S2014= =1007×（a2+a2013）=4028，
    所以答案是：4028．
    【考点精析】通过灵活运用等差数列的性质，掌握在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数 （m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为（ ）
    A.a＜b＜c
    B.b＜a＜c
    C.c＜a＜b
    D.a＜c＜b

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商品最近30天的价格f（t）（元）与时间t满足关系式：f（t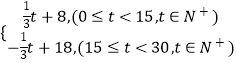）= ，且知销售量g（t）与时间t满足关系式 g（t）=﹣t+30，（0≤t≤30，t∈N+），求该商品的日销售额的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|﹣2≤x≤5}，B={x|m+1≤x≤2m﹣1}．
    （1）当m=3时，求集合A∩B，A∪B；
    （2）若BA，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对的边长分别是a，b，c．满足2acosC+ccosA=b．
    （Ⅰ）求角C的大小；
    （Ⅱ）求sinAcosB+sinB的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C对应的边分别是a，b，c且cos2B+3cosB﹣1=0．
    （1）求角B的大小；
    （2）若a+c=1，求b的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）请在直角坐标系中画出函数f（x）的图象，并写出该函数的单调区间；
    （2）若函数g（x）=f（x）﹣m恰有3个不同零点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数其中实数为常数且.

    （I）求函数的单调区间；

    （II）若函数既有极大值，又有极小值，求实数的取值范围及所有极值之和；

    （III）在（II）的条件下，记分别为函数的极大值点和极小值点，

    求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）加以统计，得到如图所示的频率分布直方图，已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为 ．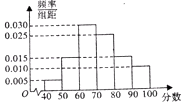

    查看答案和解析>>

    同步练习册答案