
【题目】在平面直角坐标系xOy中,已知抛物线C:x2=4y,点P是C的准线l上的动点,过点P作C的两条切线,切点分别为A,B,则△AOB面积的最小值为( )
A.![]()
B.2
C.2 ![]()
D.4
【答案】B
【解析】解:如图所示:抛物线C:x2=4y,准线l的方程y=﹣1,设P(x0 , ﹣1),A(x1 , y1),B(x2 , y2), 由y= ![]() x2 , 求导y′=
x2 , 求导y′= ![]() x,
x,
切线PA的方程为y﹣x1= ![]() x1(x﹣x1),即y=
x1(x﹣x1),即y= ![]() x1x﹣y1 ,
x1x﹣y1 ,
又切线PA过点P(x0 , ﹣1),﹣1= ![]() x1x0﹣y1 ,
x1x0﹣y1 ,
整理得:x1x0﹣2y1+2=0,
同理切线PB的方程x2x0﹣2y2+2=0,
∴直线AB的方程为xx0﹣2y+2=0,
直线AB过定点F(0,1),
∴△AOB面积,S= ![]() 丨OF丨丨x1﹣x2丨=
丨OF丨丨x1﹣x2丨= ![]() 丨x1﹣x2丨≥
丨x1﹣x2丨≥ ![]() ×4=2,
×4=2,
∴当且仅当直线AB⊥y轴时取等号,
∴△AOB面积的最小值2,
故选B.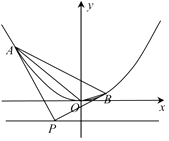


科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C的对边分别为a、b、c,且满足sinA+sinB=[cosA﹣cos(π﹣B)]sinC.
(1)试判断△ABC的形状,并说明理由;
(2)若a+b+c=1+ ![]() ,试求△ABC面积的最大值.
,试求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(Ⅰ)设为P为AC的中点,Q为AB上一点,使PQ⊥OA,并计算 ![]() 的值;
的值;
(Ⅱ)求二面角O﹣AC﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设每一架飞机的每一个引擎在飞行中出现故障概率均为![]() ,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎飞机正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机才可成功飞行.要使4引擎飞机比2引擎飞机更安全,则
,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎飞机正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机才可成功飞行.要使4引擎飞机比2引擎飞机更安全,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】爱心超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完![]() 根据往年销售经验,每天需求量与当天最高气温
根据往年销售经验,每天需求量与当天最高气温![]() 单位:
单位:![]() 有关
有关![]() 如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶
,需求量为300瓶;如果最高气温低于20,需求量为200瓶![]() 为了确定六月份的订购计划,统计了前三年六月份每天的最高气温数据,得到下面的频数分布表:
为了确定六月份的订购计划,统计了前三年六月份每天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的频率;
(2)当六月份有一天这种酸奶的进货量为450瓶时,求这一天销售这种酸奶的平均利润(单位:元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足sin2B+sin2C=sin2A+2sinBsinCsin(B+C). (Ⅰ)求角A的大小;
(Ⅱ)若a=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)平面上有两点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)若![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 分别切圆
分别切圆![]() 于
于![]() 两点,试问:直线
两点,试问:直线![]() 是否恒过定点?若是,求出定点坐标,若不是,说明理由.
是否恒过定点?若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+|x﹣a|(a∈R).
(1)若 a=1,求不等式 f(x)≥5的解集;
(2)若函数f(x)的最小值为3,求实数 a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com