
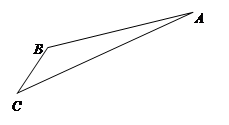
如图,游客在景点 处下山至
处下山至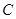 处有两条路径.一条是从
处有两条路径.一条是从 沿直道步行到
沿直道步行到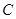 ,另一条是先从
,另一条是先从 沿索道乘缆车到
沿索道乘缆车到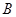 ,然后从
,然后从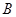 沿直道步行到
沿直道步行到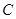 .现有甲、乙两位游客从
.现有甲、乙两位游客从 处下山,甲沿
处下山,甲沿 匀速步行,速度为
匀速步行,速度为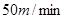 .在甲出发
.在甲出发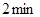 后,乙从
后,乙从 乘缆车到
乘缆车到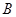 ,在
,在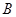 处停留
处停留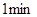 后,再从
后,再从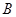 匀速步行到
匀速步行到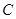 .假设缆车匀速直线运动的速度为
.假设缆车匀速直线运动的速度为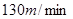 ,索道
,索道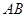 长为
长为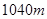 ,经测量
,经测量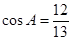 ,
,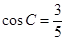 .
.
(1)求山路 的长;
的长;
(2)假设乙先到,为使乙在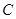 处等待甲的时间不超过
处等待甲的时间不超过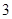 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
(1)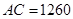 米;(2)乙步行的速度应控制在
米;(2)乙步行的速度应控制在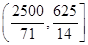
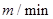 内.
内.
解析试题分析:(1)利用同角三角函数的基本关系先求出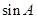 和
和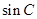 ,再利用内角和定理以及诱导公式、两角和的正弦公式求出
,再利用内角和定理以及诱导公式、两角和的正弦公式求出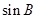 的值,最终利用正弦定理求出
的值,最终利用正弦定理求出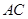 的长度;(2)利用正弦定理先求出
的长度;(2)利用正弦定理先求出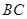 的长度,然后计算甲步行至
的长度,然后计算甲步行至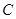 处所需的时间以及乙从
处所需的时间以及乙从 乘缆车到
乘缆车到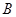 所需的时间,并设乙步行的速度为
所需的时间,并设乙步行的速度为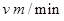 ,根据题中条件列有关
,根据题中条件列有关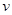 的不等式,求出
的不等式,求出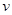 即可.
即可.
试题解析:(1)∵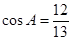 ,
,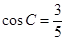 ,
,
∴ 、
、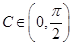 ,∴
,∴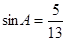 ,
,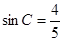 ,
,
∴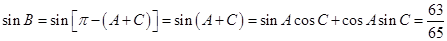 ,
,
根据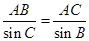 得
得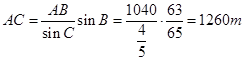 ,
,
所以山路 的长为
的长为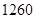 米;
米;
(2)由正弦定理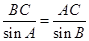 得
得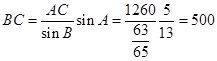 (
(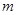 ),
),
甲共用时间: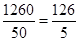 ,乙索道所用时间:
,乙索道所用时间: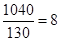 ,
,
设乙的步行速度为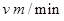 ,由题意得
,由题意得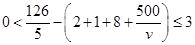 ,
,
整理得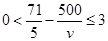 ,
,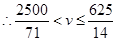 ,
,
∴为使乙在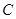 处等待甲的时间不超过
处等待甲的时间不超过 分钟,乙步行的速度应控制在
分钟,乙步行的速度应控制在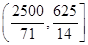
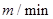 内.
内.
考点:1.同角三角函数的基本关系;2.内角和定理;3.两角和的正弦公式;4.正弦定理


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
如图,山顶有一座石塔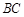 ,已知石塔的高度为
,已知石塔的高度为 .
.
(Ⅰ)若以 为观测点,在塔顶
为观测点,在塔顶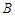 处测得地面上一点
处测得地面上一点 的俯角为
的俯角为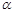 ,在塔底
,在塔底 处测得
处测得 处的俯角为
处的俯角为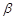 ,用
,用 表示山的高度
表示山的高度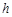 ;
;
(Ⅱ)若将观测点选在地面的直线 上,其中
上,其中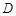 是塔顶
是塔顶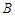 在地面上的射影.已知石塔高度
在地面上的射影.已知石塔高度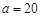 ,当观测点
,当观测点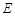 在
在 上满足
上满足 时看
时看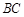 的视角(即
的视角(即 )最大,求山的高度
)最大,求山的高度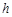 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=cos 2x+2sin x·sin.
(1)求f(x)的最小正周期,最大值以及取得最大值时x的集合;
(2)若A是锐角三角形△ABC的内角,f(A)=0,b=5,a=7,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c,且满足 (a-c)cosB=bcosC.
(1)求角B的大小;(2)若b=,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com