
【题目】全集![]() ,非空集合
,非空集合![]() ,且
,且![]() 中的点在平面直角坐标系
中的点在平面直角坐标系![]() 内形成的图形关于
内形成的图形关于![]() 轴、
轴、![]() 轴和直线
轴和直线![]() 均对称.下列命题:
均对称.下列命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() 中至少有8个元素;
中至少有8个元素;
③若![]() ,则
,则![]() 中元素的个数一定为偶数;
中元素的个数一定为偶数;
④若![]() ,则
,则![]() .
.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
科目:高中数学 来源: 题型:
【题目】【2018四川绵阳南山中学高三二诊热身考试】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩![]() 服从正态分布
服从正态分布![]() ,已知
,已知![]() ,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;
,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;
②已知命题![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
③在![]() 上随机取一个数
上随机取一个数![]() ,能使函数
,能使函数![]() 在
在![]() 上有零点的概率为
上有零点的概率为![]() ;
;
④在某次飞行航程中遭遇恶劣气候,用分层抽样的20名男乘客中有5名晕机,12名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用独立性检验,有97%以上的把握认为与性别有关.
| 0.15 | 0.1 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
其中真命题的序号为( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
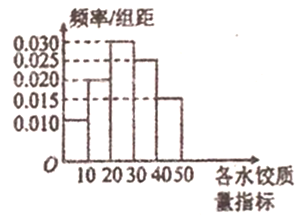
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() 是整数,且
是整数,且![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)若![]() ,
, ![]() ,写出
,写出![]() 的值;
的值;
(Ⅱ)若在数列![]() 的前2018项中,奇数的个数为
的前2018项中,奇数的个数为![]() ,求
,求![]() 得最大值;
得最大值;
(Ⅲ)若数列![]() 中,
中, ![]() 是奇数,
是奇数, ![]() ,证明:对任意
,证明:对任意![]() ,
, ![]() 不是4的倍数.
不是4的倍数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,在四边形ABCD中, ![]() ,
, ![]() 是边长为4的正三角形,把
是边长为4的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面PAC
的位置,使得平面PAC![]() 平面ACD,如图乙所示,点
平面ACD,如图乙所示,点![]() 分别为棱
分别为棱![]() 的中点.
的中点.
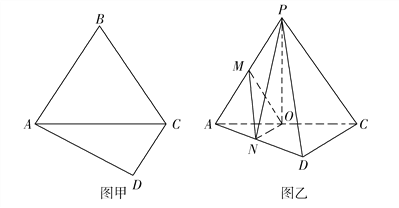
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com