
已知f(x)=x3+x(x∈R),
(1)判断f(x)在(-∞,+∞)上的单调性,并证明;
(2)求证:满足f(x)=a(a为常数)的实数x至多只有一个.
(1) f(x)=x3+x在R上是增函数
(2)见解析
【解析】(1)解:f(x)在(-∞,+∞)上是增函数.证明如下:
设x1<x2,即x1-x2<0.
∴f(x1)-f(x2)=(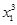 +x1)-(
+x1)-(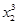 +x2)
+x2)
=(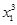 -
-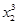 )+(x1-x2)
)+(x1-x2)
=(x1-x2)(  +x1x2+
+x1x2+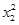 +1)
+1)
=(x1-x2)[(x1+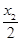 )2+
)2+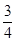
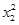 +1]<0.
+1]<0.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
因此f(x)=x3+x在R上是增函数.
(2)证明:假设x1<x2且f(x1)=f(x2)=a,由f(x)在R上递增,
∴f(x1)<f(x2),与f(x1)=f(x2)矛盾.
∴原命题正确.
点评:利用定义判断函数单调性时,通常将作差后的因式变形成因式连乘积的形式、平方和的形式等.在因式连乘积的形式中,一定含有因式“x1-x2”,这也是指导我们化简的目标.差的符号是由自变量的取值范围、假定的大小关系及符号的运算法则共同决定的.


科目:高中数学 来源:2014届浙江省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知f(x)=x3+x,若a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
A.一定大于0 B.一定等于0 C.一定小于0 D.正负都有可能
查看答案和解析>>
科目:高中数学 来源:2013届山东省高二下学期3月月考理科数学试卷(解析版) 题型:选择题
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
A、-1<a<2 B、-3<a<6 C、a<-1或a>2 D、a<-3或a>6
查看答案和解析>>
科目:高中数学 来源:2013届浙江省杭州市高二第二学期3月月考理科数学试卷 题型:选择题
已知f(x)=x3+x,若a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
A.一定大于0 B.一定等于0 C.一定小于0 D.正负都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com