
分析 (Ⅰ)求出函数f(x)的导数,解关于导函数的不等式,求出函数f(x)的最大值,证明结论即可;
(Ⅱ)问题转化为证明${(\frac{tlnt}{t-1})_{min}}>{(-f(x)-a)_{min}}$,设$h(t)=\frac{tlnt}{t-1}$,根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)当a=-1时,f(x)=lnx-x+1(x>0),
则$f'(x)=\frac{1}{x}-1=\frac{1-x}{x}$,令f'(x)=0,得x=1.
当0<x<1时,f'(x)>0,f(x)单调递增;当x>1时,f'(x)<0,f(x)单调递减.
故当x=1时,函数f(x)取得极大值,也为最大值,所以f(x)max=f(1)=0,
所以,f(x)≤0,得证.(4分)
(II)原题即对任意t≥e,存在x∈(0,+∞),使$\frac{tlnt}{t-1}>-f(x)-a$成立,
只需${(\frac{tlnt}{t-1})_{min}}>{(-f(x)-a)_{min}}$.(5分)
设$h(t)=\frac{tlnt}{t-1}$,则$h'(t)=\frac{t-1-lnt}{{{{(t-1)}^2}}}$,
令u(t)=t-1-lnt,则$u'(t)=1-\frac{1}{t}=\frac{t-1}{t}>0$对于t≥e恒成立,
所以u(t)=t-1-lnt为[e,+∞)上的增函数,
于是u(t)=t-1-lnt≥u(e)=e-2>0,即$h'(t)=\frac{t-1-lnt}{{{{(t-1)}^2}}}>0$对于t≥e恒成立,
所以$h(t)=\frac{tlnt}{t-1}$为[e,+∞)上的增函数,则$h{(t)_{min}}={(\frac{tlnt}{t-1})_{min}}=h(e)=\frac{e}{e-1}$.(8分)
令p(x)=-f(x)-a,则p(x)=-lnx-a(x-1)-a=-lnx-ax,
当a≥0时,p(x)=-lnx-ax为(0,+∞)的减函数,且其值域为R,符合题意.
当a<0时,$p'(x)=-\frac{1}{x}-a$,由p'(x)=0得$x=-\frac{1}{a}>0$,
由p'(x)>0得$x>-\frac{1}{a}$,则p(x)在$(-\frac{1}{a},+∞)$上为增函数;
由p'(x)<0得$0<x<-\frac{1}{a}$,则p(x)在$(0,-\frac{1}{a})$上为减函数,
所以$p{(x)_{min}}=p(-\frac{1}{a})=ln(-a)+1$,
从而由$ln(-a)+1<\frac{e}{{{e}-1}}$,解得$-{{e}^{\frac{1}{{{e}-1}}}}<a<0$.
综上所述,a的取值范围是$(-{{e}^{\frac{1}{{{e}-1}}}},+∞)$.(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,考查分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{10}({x}_{i}-\overline{x})^{2}$ | $\sum_{i=1}^{10}({w}_{i}-\overline{w})^{2}$ | $\sum_{i=1}^{10}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{10}({w}_{i}-\overline{w})({y}_{i}-\overline{y})$ |
| 1.63 | 37.8 | 0.89 | 5.15 | 0.92 | -20.6 | 18.40 |
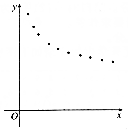 (Ⅰ)根据散点图判断,$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型?(不必说明理由)
(Ⅰ)根据散点图判断,$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型?(不必说明理由)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 30 | 40 | 50 | 60 |
| y | 25 | 30 | 40 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -200 | B. | -100 | C. | 0 | D. | -50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com