
| A. | (-5,5$\sqrt{2}$] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-5,5] | D. | [-5$\sqrt{2}$,5) |
分析 由M与N,以及两集合交集不为空集,确定出b的范围即可
解答 解:解:画出M与N中两函数图象,如图所示,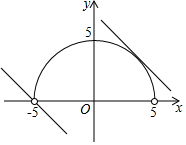
∵M={(x,y)|y=$\sqrt{25-{x}^{2}}$,y≠0},N={(x,y)|y=-x+b},且M∩N≠∅,
∴半圆y=$\sqrt{25-{x}^{2}}$与直线y=-x+b有公共点,
当直线y=-x+b与半圆相切时,圆心(0,0)到直线y=-x+b的距离d=r,即$\frac{|b|}{\sqrt{2}}$=5,
解得:b=5$\sqrt{2}$(负值舍去),
把(-5,0)代入y=-x+b得:b=-5,
则实数b的范围是(-5,5$\sqrt{5}$],
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -3 | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面β,任取直线m?α,那么必有m⊥β | |
| B. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| C. | 如果直线m∥平面α,直线n∥平面α,那么m∥n | |
| D. | 如果平面α外的一条直线m垂直于平面α内的两条相交直线,那么m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
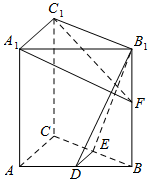 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com