
| A. | (1)(2) | B. | (2)(3) | C. | (1)(3) | D. | (2)(4) |
分析 (1),等比数列{an}单调递增时⇒公比q>1且首项a1>0,或公比0<q>1且首项a1<0;
(2),根据二项式${({2x+\frac{1}{{\sqrt{x}}}})^5}$的展开式的通项公式可得展开式中无理项项数,再用古典概型概率计算公式可求;
(3),$S=\int_0^{\frac{1}{2}}{\sqrt{\frac{1}{4}-{x^2}}}dx$表示圆x2+y2=$\frac{1}{4}$(y≥0,0≤x≤$\frac{1}{2}$)的圆的面积;
(4),1000÷40=25.
解答 解:对于(1),等比数列{an}单调递增时⇒公比q>1且首项a1>0,或公比0<q<1且首项a1<0,故错;
对于(2),二项式${({2x+\frac{1}{{\sqrt{x}}}})^5}$的展开式的通项公式为:Tr+1=${C}_{5}^{r}(2)^{5-r}{x}^{5-\frac{3}{2}r}$当r=0、2、4时为有理项,即展开式中共6项,无理项有3项,按一定次序排列,则无理项互不相邻的概率是$\frac{{{A}_{3}^{3}A}_{4}^{3}}{{A}_{6}^{6}}$=$\frac{1}{5}$,故正确;
对于(3),$S=\int_0^{\frac{1}{2}}{\sqrt{\frac{1}{4}-{x^2}}}dx$表示圆x2+y2=$\frac{1}{4}$(y≥0,0≤x≤$\frac{1}{2}$)的圆的面积,则$S=\frac{π}{16}$,故正确;
对于(4),为了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为25,故错.
故选:B.
点评 本题考查了命题真假的判定,涉及到了大量的基础知识,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {x|0≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
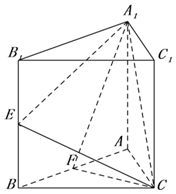 正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.
正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
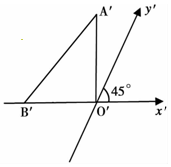 如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=8,则△AOB的边OB上的高为16$\sqrt{2}$.
如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=8,则△AOB的边OB上的高为16$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com