
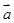 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°),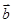 =(-
=(- ,
, ).
).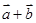 与
与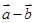 垂直;
垂直;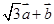 与
与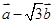 的模相等时,求角α.
的模相等时,求角α.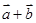 与
与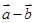 垂直,则利用数量积为零即可。
垂直,则利用数量积为零即可。 a+b|=|a-
a+b|=|a- b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。
b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。 ,sinα+
,sinα+ )·(cosα+
)·(cosα+ ,sinα-
,sinα- )
) )(cosα+
)(cosα+ )+(sinα+
)+(sinα+ )(sinα-
)(sinα- )
)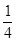 +sin2α-
+sin2α-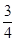 =0,
=0, a+b|=|a-
a+b|=|a- b|,平方得(
b|,平方得( a+b)2=(a-
a+b)2=(a- b)2,
b)2, ab=0①.
ab=0①. ,
, )=-
)=- cosα+
cosα+ sinα=0,即cos(60°+α)=0.
sinα=0,即cos(60°+α)=0.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源:不详 题型:填空题
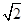 sinB-cosC的取值范围为___________.
sinB-cosC的取值范围为___________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com