解:(1)函数定义域为(-1,+∞),∵
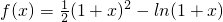
∴f′(x)=
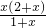
,
由f'(x)>0及x>-1,得x>0,由f'(x)<0及x>-1,得-1<x<0.
则递增区间是(0,+∞),递减区间是(-1,0);
(2)由f′(x)=
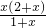
=0,得x=0或x=-2
由(1)知,f(x)在[

-1,0]上递减,在[0,e-1]上递增
又f(

-1)=
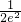
+1,f(e-1)=

-1,

-1>
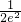
+1
∴x∈[

-1,e-1]时,[f(x)]
max=

-1,
∴m>

-1时,不等式f(x)<m恒成立;
(3)由
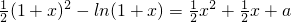
得2a=(1+x)-2ln(1+x)
令h(x)=(1+x)-2ln(1+x),则h′(x)=

∴h(x)在[0,1]上单调递减,在[1,2]上单调递增
∵h(0)=1,h(1)=2-2ln2,h(3)=3-2ln3,且h(1)>h(2)>h(1)
∴当2a∈(2-2ln2,3-2ln3),即a∈(1-ln2,

-ln3)时,g(x)的图象与f(x)的图象在区间[0,2]上有两个交点.
分析:(1)先求函数的定义域,然后求导函数,令导数大于0(小于0),从而求出函数的单调区间;
(2)由(1)得f(x)在 x∈[

-1,e-1]的单调性,进一步求出f(x)
max,得到m的范围;
(3)由
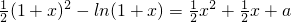
得2a=(1+x)-2ln(1+x),构造函数,确定函数的值域,即可求得a的取值范围.
点评:本题以函数为载体,考查函数的单调性,考查函数的最值.解决不等式恒成立求参数的范围,一般是将参数分离出来,通过构造函数,利用导数求出函数的单调性进一步求出函数的最值,得到参数的范围.

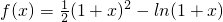
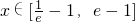 时,f(x)<m恒成立,求m的取值范围;
时,f(x)<m恒成立,求m的取值范围;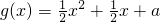 ,若g(x)的图象与f(x)的图象在区间[0,2]上有两个交点,求a的取值范围.
,若g(x)的图象与f(x)的图象在区间[0,2]上有两个交点,求a的取值范围.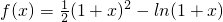 ∴f′(x)=
∴f′(x)=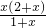 ,
,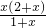 =0,得x=0或x=-2
=0,得x=0或x=-2 -1,0]上递减,在[0,e-1]上递增
-1,0]上递减,在[0,e-1]上递增 -1)=
-1)=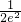 +1,f(e-1)=
+1,f(e-1)= -1,
-1, -1>
-1>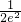 +1
+1 -1,e-1]时,[f(x)]max=
-1,e-1]时,[f(x)]max= -1,
-1, -1时,不等式f(x)<m恒成立;
-1时,不等式f(x)<m恒成立;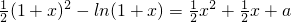 得2a=(1+x)-2ln(1+x)
得2a=(1+x)-2ln(1+x)
 -ln3)时,g(x)的图象与f(x)的图象在区间[0,2]上有两个交点.
-ln3)时,g(x)的图象与f(x)的图象在区间[0,2]上有两个交点. -1,e-1]的单调性,进一步求出f(x)max,得到m的范围;
-1,e-1]的单调性,进一步求出f(x)max,得到m的范围;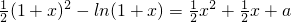 得2a=(1+x)-2ln(1+x),构造函数,确定函数的值域,即可求得a的取值范围.
得2a=(1+x)-2ln(1+x),构造函数,确定函数的值域,即可求得a的取值范围.

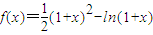
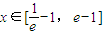 时,f(x)<m恒成立,求m的取值范围;
时,f(x)<m恒成立,求m的取值范围;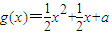 ,若g(x)的图象与f(x)的图象在区间[0,2]上有两个交点,求a的取值范围.
,若g(x)的图象与f(x)的图象在区间[0,2]上有两个交点,求a的取值范围.