
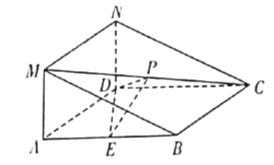
【题目】在如图所示的几何体中,四边形![]() 是菱形,四边形
是菱形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的一点.
上的一点.
(1)求证:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)连接DB,由已知可得△ABD为等边三角形,得到DE⊥AB,则DE⊥DC,再由ADNM为矩形,得DN⊥AD,由面面垂直的性质可得DN⊥平面ABCD,得到DN⊥DE,由线面垂直的判断可得DE⊥平面DCN,进一步得到DE⊥CN;
(2)由(1)知DN⊥平面ABCD,得到DN⊥DE,DN⊥DC,又DE⊥DC,以D为坐标原点,DE、DC、DN分别为x轴、y轴、z轴建立空间直角坐标系,设![]() ,λ∈[0,1],分别求出平面PDE与平面DEC的一个法向量,由二面角P﹣DE﹣C的大小为
,λ∈[0,1],分别求出平面PDE与平面DEC的一个法向量,由二面角P﹣DE﹣C的大小为![]() 列式求得λ即可.
列式求得λ即可.
(1)连接![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,
,
![]() 为等边三角形.
为等边三角形.
又![]() 为
为![]() 的中点,
的中点,![]() .
.
又![]() ,
,![]() .
.
![]() 四边形
四边形![]() 为矩形,
为矩形,![]() .
.
又![]() 平面
平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .
.
又![]()
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 。
。
![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,

则![]() ,
,
![]() ,
,
设![]() ,
,
则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,
,
即 ,
,
令![]() ,则
,则![]() .
.
由图形知,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,
,
即 ,即
,即![]() .
.
![]() ,
,
![]() 解得
解得![]() ,
,![]() 的值为
的值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】西安市自2017年5月启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,斑马线前礼让行人也成为了一张新的西安“名片”.
但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患及机动车通畅率降低,交警部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到![]() 列联表如下:
列联表如下:
30岁以下 | 30岁以上 | 合计 | |
闯红灯 | 60 | ||
未闯红灯 | 80 | ||
合计 | 200 |
近期,为了整顿“行人闯红灯”这一不文明及项违法行为,交警部门在该十字路口试行了对闯红灯行人进行经济处罚,并从试行经济处罚后穿越该路口行人中随机抽取了200人进行调查,得到下表:
处罚金额 | 5 | 10 | 15 | 20 |
闯红灯的人数 | 50 | 40 | 20 | 0 |
将统计数据所得频率代替概率,完成下列问题.
(Ⅰ)将![]() 列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
(Ⅱ)当处罚金额为10元时,行人闯红灯的概率会比不进行处罚降低多少;
(Ⅲ)结合调查结果,谈谈如何治理行人闯红灯现象.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.132 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年冬奥会,某市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如图所示的茎叶图:
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如图所示的茎叶图:

(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核为优秀的概率;
(2)从图中考核成绩满足![]() 的学生中任取3人,设
的学生中任取3人,设![]() 表示这3人中成绩满足
表示这3人中成绩满足![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据以往培训数据,规定当![]() 时培训有效.请你根据图中数据,判断此次冰雪培训活动是否有效,并说明理由.
时培训有效.请你根据图中数据,判断此次冰雪培训活动是否有效,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
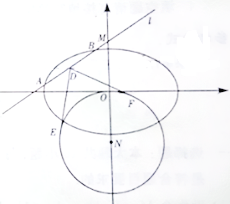
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,椭圆C截直线y=1所得线段的长度为
,椭圆C截直线y=1所得线段的长度为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求![]() EDF的最小值.
EDF的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

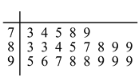
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
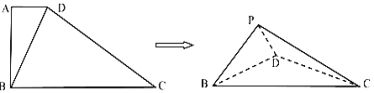
【题目】如图,在直角梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,将直角梯形
,将直角梯形![]() 沿对角线
沿对角线![]() 折起,使点
折起,使点![]() 到
到![]() 点位置,则四面体
点位置,则四面体![]() 的体积的最大值为________,此时,其外接球的表面积为________.
的体积的最大值为________,此时,其外接球的表面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与过点
与过点![]() 的直线
的直线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,探究:以
,探究:以![]() 为直径的圆是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
为直径的圆是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
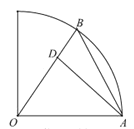
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com