
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
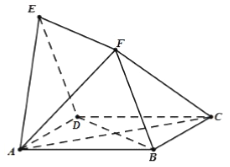
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由线面垂直的判定定理得到结论;(2)通过证明线线平行,得到线面平行;(3)建立空间直角坐标系![]() ,求出平面
,求出平面![]() 的法向量,易知
的法向量,易知![]() 面
面![]() ,所以面
,所以面![]() 的法向量为
的法向量为![]() ,再求出它们的夹角的余弦值.
,再求出它们的夹角的余弦值.
试题解析:(1)证明:设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() ,且
,且![]() 为
为![]() 中点,又
中点,又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)证明:因为四边形![]() 与
与![]() 均为菱形,
均为菱形,
所以![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(3)解:因为四边形![]() 为菱形,且
为菱形,且![]() ,所以△
,所以△![]() 为等边三角形,
为等边三角形,
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,故
,故![]() 平面
平面![]() .
.
由![]() ,
,![]() ,
,![]() 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系![]() .
.
设![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形,![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则有
,则有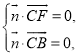 所以
所以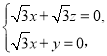
取![]() ,得
,得![]() .
.
易知平面![]() 的法向量为
的法向量为![]() .
.
由二面角![]() 是锐角,得
是锐角,得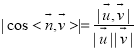
![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】用数字0、2、3、4、6按下列要求组数、计算:
(1)能组成多少个没有重复数字的三位数?
(2)可以组成多少个可以被3整除的没有重复数字的三位数?
(3)求![]() 即144的所有正约数的和.
即144的所有正约数的和.
(注:每小题结果都写成数据形式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远。其中有一题:今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何? 译文如下:要测量海岛上一座山峰![]() 的高度
的高度![]() ,立两根高均为
,立两根高均为![]() 丈的标杆
丈的标杆![]() 和
和![]() ,前后标杆相距
,前后标杆相距![]() 步,使后标杆杆脚
步,使后标杆杆脚![]() 与前标杆杆脚
与前标杆杆脚![]() 与山峰脚
与山峰脚![]() 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点共线,从后标杆杆脚
三点共线,从后标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点也共线,问岛峰的高度
三点也共线,问岛峰的高度![]() 步. (古制:
步. (古制:![]() 步=
步=![]() 尺,
尺,![]() 里=
里=![]() 丈=
丈=![]() 尺=
尺=![]() 步)
步)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
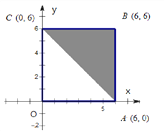
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 短轴顶点在圆
短轴顶点在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 方程;
方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究以
两点,试探究以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心是坐标原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为![]() .过右焦点
.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.
两点.
(1)求椭圆的方程;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,请
的取值范围;若不存在,请
说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com