Question

判断下列函数的单调性,并说明理由.

(1)y=;

(2)y=x²-2|x|-1.

Answer 1

思路分析:判断函数的单调性,首先必须确定函数的定义域,而后在定义域内确定单调递增、递减区间.含绝对值的函数应先将原函数化为分段函数,在各自的分段区间内确定递增、递减区间.

解:(1)由题意3-2x-x²≥0,解得-3≤x≤1,

故函数y=的定义域是[-3,1].

∵3-2x-x²=-(x+1)₂+4,

∴由二次函数的性质可知,此函数在[-3,-1] 上是增函数,在[-1,1]是减函数.

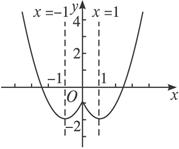
           图1-3-3

(2)由题意,y=x²-2|x|-1=x²-2x-1=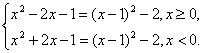

它的图象如图1-3-3所示,可知此函数在区间(-∞,-1和[0,1]上是减函数,在区间[-1, 0]和-∞,-1)上是增函数.

说明:利用基本函数的单调性及函数的图象是判定函数单调性的常用方法.对于(1),是一个复合函数求单调性的问题,y=可以看作是由y=和u=3-2x-x²两个函数复合而成的函数,由基本函数的性质可以得到复合函数的性质.

若u=g(x)在[a,b]上是单调增(减)函数,y=f(u)在区间[g(a),g(b)]或[g(b),g(a)]上是单调增(减)函数,那么复合函数y= y=f[a,b]在[a,b]上一定是单调函数,并且有以下结论.

函数	u=g(x)	y=f(u)	y=f[g(x)]
函数的单调性	增函数	增函数	增函数
	增函数	减函数	减函数
	减函数	增函数	减函数
	减函数	减函数	增函数

这一规律类似于我们熟悉的正负数的乘法符号法则,事实上,如果把“增”看成“正”,把“减”看成“负”,则“正正为正”,“负负为正”,分别与“增增为增”,“减减为减”相类似;“正负为负”,“负正为负”分别与“增减为减”,“减增为减”相类似,这样一来,就容易记住了.

判断函数的单调性应在定义域的范围内,本题易忽视定义域,这将导致解题失误,因为单调性是在定义域内定义的.