
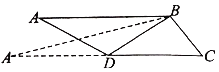
【题目】如图,△ABC中,AB⊥BC,∠ACB=60°,D为AC中点,△ABD沿BD翻折过程中,直线AB与直线BC所成的最大角、最小角分别记为α1,β1,直线AD与直线BC所成最大角、最小角分别记为α2,β2,则有( )
A.α1<α2,β1≤β2B.α1<α2,β1>β2
C.α1≥α2,β1≤β2D.α1≥α2,β1>β2
【答案】D
【解析】
翻折到180°时,AB,BC所成角最小,β1=30°,AD,BC所成角最小,β2=0°,翻折0°时,AB,BC所成角最大,可知α1=90°,翻折过程中,可知AD的投影可与BC垂直,从而AD,BC所成最大角α2=90°,推导出α1=90°,β1=30°,α2=90°,β2=0°.
翻折到180°时,AB,BC所成角最小,可知β1=30°,
![]() ,AD,BC所成角最小,β2=0°,
,AD,BC所成角最小,β2=0°,
翻折0°时,AB,BC所成角最大,可知α1=90°,
翻折过程中,可知AD的投影可与BC垂直,
所以AD,BC所成最大角α2=90°,
所以α1=90°,β1=30°,α2=90°,β2=0°.
故α1≥α2,β1>β2.
故选:D.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于![]() 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 平面ABCD,E为PD的中点,
平面ABCD,E为PD的中点,![]() .
.
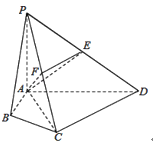
(1)求四棱锥![]() 的体积V;
的体积V;
(2)若F为PC的中点,求证:平面![]() 平面AEF;
平面AEF;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点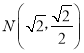 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直角梯形
,直角梯形![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com