【题目】如图1，在矩形
中，
，
，点
、
分别在线段
、
上，且
，
，现将
沿
折到
的位置，连结
，
，如图2
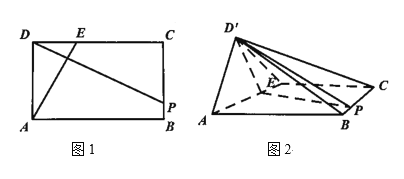
（1）证明：
；
（2）记平面
与平面
的交线为
.若二面角
为
，求与平面
所成角的正弦值.
【答案】（1）证明见解析 （2）
【解析】
(1)建立坐标系证明
，再由线面垂直的判定定理以及线面垂直的性质证明
；
(2)根据公理
得到平面
与平面
的交线，再根据二面角定义得到二面角
的平面角，建立空间直角坐标系，利用向量法求
与平面
所成角的正弦值.
解：（1）证明：如图
，线段
交于点
在
中，由
，
，
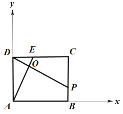
以点A为坐标原点，建立直角坐标系，则
，
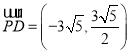
即
，从而有
，
，
即在图2中有
，，
，
平面
平面
平面，
；
（2）延长
，
交于点
，连接
根据公理得到直线即为，再根据二面角定义得到
.
在平面
内过点作底面垂线，为原点，分别以
、
、及所作为
轴、
轴、
轴建立空间直角坐标
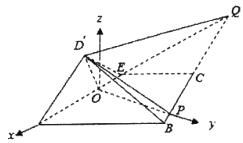
则
，
，
，
，
，
，
，
设平面
的一个法向量为
，
由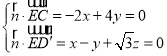
，
取
，得
.
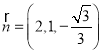与平面
所成角的正弦值为
.
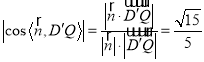阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率
，且椭圆过点
.
（1）求椭圆
的标准方程；
（2）设直线
与交于
，
两点，点
在上，
是坐标原点，若
，判断四边形
的面积是否为定值？若为定值，求出该定值；如果不是，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公园有个池塘，其形状为直角△ABC，
，AB的长为2百米，BC的长为1百米.
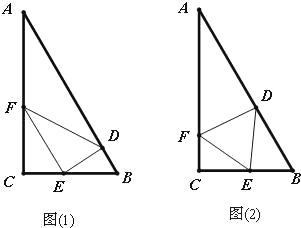
（1）若准备养一批供游客观赏的鱼，分别在AB、BC、CA上取点D、E、F，如图（1），使得
，
，在△DEF内喂食，求当△DEF的面积取最大值时EF的长；
（2）若准备建造一个荷塘，分别在AB、BC、CA上取点D、E、F，如图（2），建造△DEF连廊（不考虑宽度）供游客休憩，且使△DEF为正三角形，记
，求△DEF边长的最小值及此时
的值.（精确到1米和0.1度）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知袋中装有红球，黑球共7个，若从中任取两个小球（每个球被取到的可能性相同），其中恰有一个红球的概率为
.
（1）求袋中红球的个数；
（2）若袋中红球比黑球少，从袋中任取三个球，求三个球中恰有一个红球的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“共享单车”的出现，为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的
城市和交通拥堵严重的
城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如图：
（1）根据茎叶图，比较两城市满意度评分的平均值的大小（不要求计算具体值，给出结论即可）；
（2）若得分不低于85分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此列联表，并据此样本分析是否有
的把握认为城市拥堵与认可共享单车有关；
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
（3）若此样本中的城市和城市各抽取1人，则在此2人中恰有一人认可的条件下，此人来自城市的概率是多少？
（参考公式：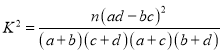
）
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
极坐标系的极点为直角坐标系
的原点，极轴为
轴的正半轴，两种坐标系中的长度单位相同，已知曲线
的极坐标方程为
.
（1）求
的直角坐标方程；
（2）直线
（
为参数）与曲线
交于
两点，与
轴交于
，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】经观测，某公路段在某时段内的车流量
(千辆/小时)与汽车的平均速度
(千米/小时)之间有函数关系：
．
（1）在该时段内，当汽车的平均速度为多少时车流量最大？最大车流量为多少？(精确到0.01)
（2）为保证在该时段内车流量至少为10千辆/小时，则汽车的平均速度应控制在什么范围内？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知梯形
中，
，
，
，四边形
为矩形，
，平面
平面．
（Ⅰ）求证：
平面
；
（Ⅱ）求平面与平面
所成锐二面角的余弦值；
（Ⅲ）在线段
上是否存在点
，使得直线
与平面所成角的正弦值为
，若存在，求出线段的长；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
