
【题目】2016年10月28日,经历了近半个世纪风雨的南京长江大桥真“累”了,终于停下来喘口气了,之前大桥在改善我们城市的交通状况方面功不可没.据相关数据统计,一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到280辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过30辆/千米时,车流速度为50千米/小时.研究表明,当30≤x≤280时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤280时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) f(x)=xv(x)可以达到最大,并求出最大值.
【答案】
(1)解:由题意,得当0≤x≤30时,v(x)=50;
当30<x≤280时,
设v(x)=ax+b.
由已知 ![]() ,解得a=﹣0.2,b=56,
,解得a=﹣0.2,b=56,
故函数v(x)的表达式为v(x)= ![]()
(2)解:f(x)=xv(x)= ![]() ,
,
当0≤x≤30时,f(x)≤1500.
当30<x≤280时,f(x)=﹣0.2(x﹣140)2+3920,∴x=140,f(x)max=3920
∴车流密度x为140,f(x)=xv(x)可以达到最大为3920
【解析】(1)设v(x)=ax+b.利用x的范围,列出方程组求解a,b,即可得到函数的解析式.(2)求出车流量f(x)=v(x)x的表达式,然后求解最大值即可.


科目:高中数学 来源: 题型:
【题目】如图,一条河的两岸平行,河的宽度d=600m,一艘客船从码头A出发匀速驶往河对岸的码头B.已知|AB|=1km,水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟,则客船在静水中的速度大小为( )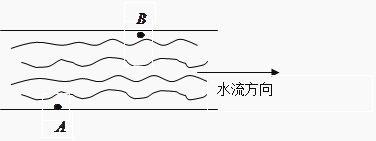
A.8km/h
B.![]() km/h
km/h
C.![]() km/h
km/h
D.10km/h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①向量 ![]() 与
与 ![]() 是共线向量,则A、B、C、D必在同一直线上;
是共线向量,则A、B、C、D必在同一直线上;
②向量 ![]() 与向量
与向量 ![]() 平行,则
平行,则 ![]() 方向相同或相反;
方向相同或相反;
③若下列向量 ![]() 、
、 ![]() 满足
满足 ![]() ,且
,且 ![]() 与
与 ![]() 同向,则
同向,则 ![]() ;
;
④若 ![]() ,则
,则 ![]() 的长度相等且方向相同或相反;
的长度相等且方向相同或相反;
⑤由于零向量方向不确定,故不能与任何向量平行.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在平面直角坐标系中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线![]() 的参数方程为
的参数方程为 ;曲线
;曲线![]() 的极坐标方程为
的极坐标方程为![]() ;曲线
;曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程、曲线
的直角坐标方程、曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 曲线
曲线![]() 在第一象限的交点分别为
在第一象限的交点分别为![]() ,求
,求![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且 ![]()
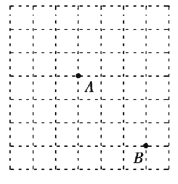
(1)画出所有的向量 ![]() ;
;
(2)求| ![]() |的最大值与最小值.
|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-(a+2)x+ln x.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com