
【题目】设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线![]()
(1)求φ;
(2)求函数y=f(x)的单调递增区间;
(3)求函数y=f(x)在区间![]() 上的值域。
上的值域。
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形, ![]() 为直角三角形,
为直角三角形, ![]() ,且
,且![]() .
.
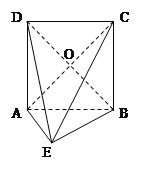
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61,
(1)求a与b的夹角θ; (2)求|a+b|;
(3)若![]() =a,
=a, ![]() =b,求△ABC的面积.
=b,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
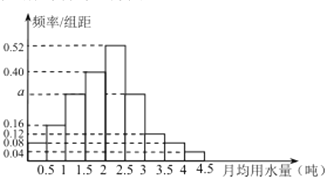
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本x1,x2,…,x10数据的平均值和方差分别为3和5,若yi=xi+a(a为非零实数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( )
A. 3,5 B. 3+a,5 C. 3+a,5+a D. 3,5+a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若存在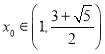 ,使函数
,使函数![]() 的图像在点
的图像在点![]() 和点
和点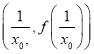 处的切线互相垂直,求
处的切线互相垂直,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 在区间
在区间![]() 上有两个极值点,则是否存在实数
上有两个极值点,则是否存在实数![]() ,使
,使![]() 对任意的
对任意的![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com