
如图,在△ACB中,∠ACB = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以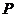 为圆心,1为半径作
为圆心,1为半径作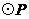 .
.
(1)连结 ,若
,若 ,试判断
,试判断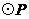 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;
(2)当线段PC等于多少时,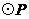 与直线AB相切?
与直线AB相切?
(3)当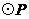 与直线AB相交时,写出线段PC的取值范围。
与直线AB相交时,写出线段PC的取值范围。
(第(3)问直接给出结果,不需要解题过程)

科目:高中数学 来源: 题型:
 如图,在几何体中,四边形ABCD为平行四边形,且∠ACB=90°,平面ACE⊥平面ABCD,EF∥BC,AC=BC=2,AE=EC=
如图,在几何体中,四边形ABCD为平行四边形,且∠ACB=90°,平面ACE⊥平面ABCD,EF∥BC,AC=BC=2,AE=EC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•和平区三模)如图,在△ABC中,∠ABC=∠ACB=30°,AB,AC边上的高分别为CD,BE,则以B,C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为
(2008•和平区三模)如图,在△ABC中,∠ABC=∠ACB=30°,AB,AC边上的高分别为CD,BE,则以B,C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012年江苏省高一上学期开学考试数学 题型:解答题
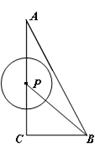
(本题共9分)如图,在△ACB中,∠ACB = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以 为圆心,1为半径作
为圆心,1为半径作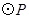 .
.
(1)连结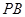 ,若
,若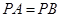 ,试判断
,试判断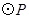 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;
(2)当线段PC等于多少时,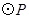 与直线AB相切?
与直线AB相切?
(3)当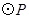 与直线AB相交时,写出线段PC的取值范围。
与直线AB相交时,写出线段PC的取值范围。
(第(3)问直接给出结果,不需要解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com