
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(Ⅰ)若![]() ,求以
,求以![]() 为直径的圆被
为直径的圆被![]() 轴所截得的弦长;
轴所截得的弦长;
(Ⅱ)分别过点![]() 作抛物线
作抛物线![]() 的切线,两条切线交于点
的切线,两条切线交于点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】已知双曲线E![]() 的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
A.y=±![]() B.y=±
B.y=±![]() C.y=±2xD.y=±3x
C.y=±2xD.y=±3x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本![]() (万元)与处理量
(万元)与处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:
![]() ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为![]() 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴![]() 万元.
万元.
(1)当![]() 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
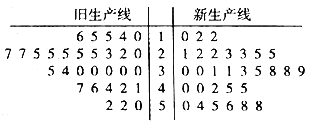
【题目】近几年,我国鲜切花产业得到了快速发展,相关部门制定了鲜切花产品行业等级标准,统一使用综合指标值![]() 进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
(Ⅰ)根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度(直接给出结论即可);
(Ⅱ)若从等级为三级的样品中随机选取3个进行生产流程调查,其中来自新型生产线的样品个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根据该花卉生产基地的生产记录,原有生产线加工的产品的单件平均利润为4元,产品的销售率(某等级产品的销量与产量的比值)及产品售价如下表:
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为span>10元,日产量3000件.因为鲜切花产品的保鲜特点,未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑,该生产基地是否需要引进该新型生产线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l的参数方程是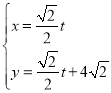 (t为参数),以O为极点,x轴正半轴为极轴的极坐标系中,圆C的极坐标方程为
(t为参数),以O为极点,x轴正半轴为极轴的极坐标系中,圆C的极坐标方程为![]() .
.
(1)求直线l的普通方程和圆C的直角坐标方程;
(2)由直线l上的点向圆C引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成6组:第1组
之间,将测量结果按如下方式分成6组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
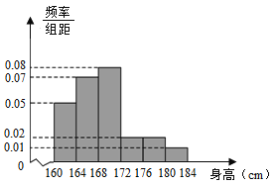
(1)由频率分布直方图估计该校高三年级男生身高的中位数;
(2)在这50名男生身高不低于![]() 的人中任意抽取2人,则恰有一人身高在
的人中任意抽取2人,则恰有一人身高在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com