
分析 根据题意,将M中所有非空子集分类考虑完备,将所有非空子集中的含有1的总个数确定好,从而可求其和,同理求得含有2、3…10的部分的和,问题即可解决.
解答 解:∵M={x|1≤x≤10,x∈N}={1,2,…10},
∴M中所有非空子集中含有1的有10类:
①单元素集合只有{1}含有1,即1出现了C90次;
②双元素集合有1的有{1,2},{1,3},…{1,10},即1出现了C91次;
③三元素集合中含有1的有{1,2,3},{1,2,4},…{1,9,10}即1出现了C92次;
…
⑩含有十个元素{1,2,…}1出现了C99次;
∴1共出现C90+C91+…+C99=29;
同理2,3,4,…10各出现29次,
∴M的所有非空子集中,这些和的总和是 29•[(-1)1+2×(-1)2+…+10×(-1)10]=29×5=2560.
故答案为:2560.
点评 本题考查与集合有关的新定义,难点在于将M中所有非空子集合理分类计算,用组合数性质解决,考查学生综合分析与推理的能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | $\frac{{8\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sina)>f(cosb) | B. | f(sina)<f(cosb) | C. | f(cosa)<f(cosb) | D. | f(cosa)>f(cosb) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{88}{41}$ | C. | $\frac{28}{17}$ | D. | $\frac{48}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
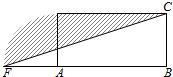 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com