
【题目】如图,已知四棱锥![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .
.
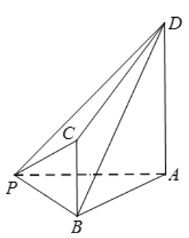
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,要证
,要证![]() 平面
平面![]() ,需证明
,需证明![]() ,
,![]() ,其中可通过证明
,其中可通过证明![]() 平面
平面![]() 来证明
来证明![]() ,通过证明
,通过证明![]() 平面
平面![]() 来证明
来证明![]() ;
;
(2)以A为坐标原点,建立空间直角坐标系,求出面![]() 的一个法向量以及直线
的一个法向量以及直线![]() 的方向向量,求出两向量的夹角的余弦值即为直线
的方向向量,求出两向量的夹角的余弦值即为直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() .
.
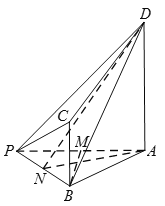
因![]() ,
,![]() 为
为![]() 的中点,
的中点,
故![]() .
.
同理,![]() ,
,![]() .
.
故![]() 平面
平面![]() .
.
故![]() .
.
因平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
故![]() 平面
平面![]() .
.
则![]() .
.
又![]() ,
,![]() 是平面
是平面![]() 中的相交直线,
中的相交直线,
故![]() 平面
平面![]() .
.
(2)由(1)知,![]() 面
面![]() ,又
,又![]() ∥
∥![]() ,
,
![]() 面
面![]() .
.
如图,以A为坐标原点,建立空间直角坐标系,
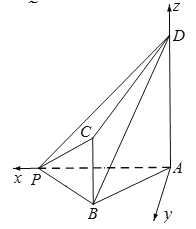
不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设![]() 是面
是面![]() 的一个法向量,
的一个法向量,
则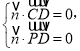 ,即
,即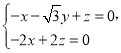 ,
,
取![]() ,则
,则![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则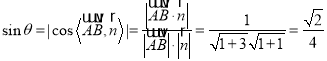 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}满足:a3+a8=20,且a5是a2与a14的等比中项.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为![]() (
(![]() 为常数)元,之后每年会投入一笔研发资金,
为常数)元,之后每年会投入一笔研发资金,![]() 年后总投入资金记为
年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() 为常数,
为常数,![]() .已知
.已知![]() 年后总投入资金为研发启动时投入资金的
年后总投入资金为研发启动时投入资金的![]() 倍.问
倍.问
(1)研发启动多少年后,总投入资金是研发启动时投入资金的![]() 倍;
倍;
(2)研发启动后第几年的投入资金的最多.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数的一个“可等域区间”.给出下列四个函数:
为函数的一个“可等域区间”.给出下列四个函数:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中存在唯一“可等域区间”的“可等域函数”的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OM,ON是两条海岸线,Q为海中一个小岛,A为海岸线OM上的一个码头.已知![]() ,
,![]() ,Q到海岸线OM,ON的距离分别为3 km,
,Q到海岸线OM,ON的距离分别为3 km,![]() km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
km.现要在海岸线ON上再建一个码头,使得在水上旅游直线AB经过小岛Q.
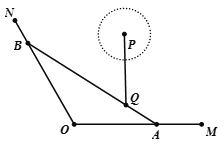
(1)求水上旅游线AB的长;
(2)若小岛正北方向距离小岛6 km处的海中有一个圆形强水波P,从水波生成t h时的半径为![]() (a为大于零的常数).强水波开始生成时,一游轮以
(a为大于零的常数).强水波开始生成时,一游轮以![]() km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.
km/h的速度自码头A开往码头B,问实数a在什么范围取值时,强水波不会波及游轮的航行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,四边形ABCD菱形,![]() ,平面
,平面![]() 平面 ABCD,
平面 ABCD,![]() .E,F 分别是线段 SC,AB 上的一点,
.E,F 分别是线段 SC,AB 上的一点, ![]() .
.
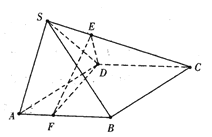
(1)求证:![]() 平面SAD;
平面SAD;
(2)求平面DEF与平面SBC所成锐二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com