
【题目】如图,设![]() 是棱长为
是棱长为![]() 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有![]() 个顶点;②有
个顶点;②有![]() 条棱;③有
条棱;③有![]() 个面;④表面积为
个面;④表面积为![]() ;⑤体积为
;⑤体积为![]() .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)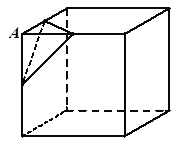
【答案】①②⑤
【解析】
解:如图,
原来的六个面还在只不过是变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,所以总计6+8=14个面,故③错;
每个正方形4条边,每个三角形3条边,4×6+3×8=48,考虑到每条边对应两个面,所以实际只有![]() ×48=24条棱.②正确;
×48=24条棱.②正确;
所有的顶点都出现在原来正方体的棱的中点位置,
原来的棱的数目是12,所以现在的顶点的数目是12.
或者从图片上可以看出每个顶点对应4条棱,每条棱很明显对应两个顶点,所以顶点数是棱数的一半即12个.①正确;
三角形和四边形的边长都是![]() a,所以正方形总面积为6×
a,所以正方形总面积为6×![]() ×a2=3a2,三角形总面积为8×
×a2=3a2,三角形总面积为8×![]() ×
×![]() a2sin60°=
a2sin60°=![]() a2,表面积(3+
a2,表面积(3+![]() )a2,故④错;
)a2,故④错;
体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×![]() (
(![]() )3=
)3=![]() a2,剩余总体积为a3-
a2,剩余总体积为a3-![]() a3=
a3=![]() a3⑤正确.
a3⑤正确.
故答案为:①②⑤.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】某地的出租车价格规定:起步费![]() 元,可行
元,可行![]() 公里,
公里,![]() 公里以后按每公里
公里以后按每公里![]() 元计算,可再行
元计算,可再行![]() 公里;超过
公里;超过![]() 公里按每公里
公里按每公里![]() 元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定。
元计算,假设不考虑堵车和红绿灯等所引起的费用,也不考虑实际收取费用去掉不足一元的零头等实际情况,即每一次乘车的车费由行车里程唯一确定。
(1)若小明乘出租车从学校到家,共![]() 公里,请问他应付出租车费多少元?
公里,请问他应付出租车费多少元?
(2)求车费![]() (元)与行车里程
(元)与行车里程![]() (公里)之间的函数关系式
(公里)之间的函数关系式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面为矩形的四棱锥![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
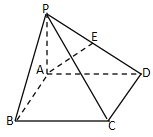
(1)求四棱锥![]() 的体积;
的体积;
(2)求![]() 与面
与面![]() 所成角;
所成角;
(3)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求出;若不存在,请说明理由.
?若存在,求出;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
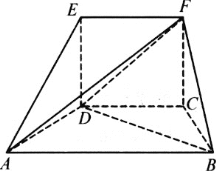
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2012年至2018年生活垃圾无害化处理量(单位:万吨)的折线图.
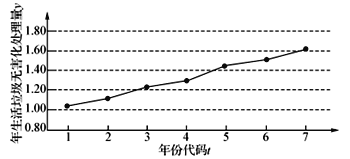
注:年份代码![]() 分别表示对应年份
分别表示对应年份![]() .
.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() (
(![]() 线性相关较强)加以说明;
线性相关较强)加以说明;
(2)建立![]() 与
与![]() 的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(参考公式)相关系数 ,在回归方程
,在回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() , O为DE的中点,
, O为DE的中点,![]() .F为
.F为![]() 的中点,平面
的中点,平面![]() 平面BCED.
平面BCED.

(1)求证:平面 ![]() 平面
平面![]() .
.
(2)线段OC上是否存在点G,使得![]() 平面EFG?说明理由。
平面EFG?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com