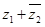Question

已知a为实数，复数z₁＝2－i，z₂＝a＋i(i为虚数单位)．
（1）若a＝1，指出在复平面内对应的点所在的象限；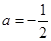
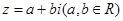（2）若z₁·z₂为纯虚数，求a的值．

Answer 1

（1）第四象限（2）

试题分析：（1）复数与复平面内点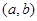一一对应，要确定复数在复平面内对应的点所在的象限，关键在于正确求出复数.由于互为共轭的两个复数，实部相等，虚部相反，所以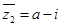，因此z₁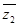＋＝(2－i)＋(1－i)＝3－2i，所以z₁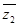＋在复平面内对应的点为(3，－2)，在第四象限，（2）复数为纯虚数，有两个条件，一是实部为零，二是虚部不为零.由z₁·z₂＝(2－i)(a＋i)＝(2a＋1)＋(2－a)i得2a＋1＝0，且2－a≠0，解得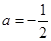
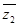试题解析：
（1）因为a＝1，
所以z₁＋＝(2－i)＋(1－i)＝3－2i．                      2分
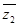所以z₁＋在复平面内对应的点为(3，－2)，
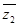从而z₁＋在复平面内对应的点在第四象限．               4分
（2）z₁·z₂＝(2－i)(a＋i)＝(2a＋1)＋(2－a) i．                  6分
因为a∈R，z₁·z₂为纯虚数，
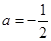所以2a＋1＝0，且2－a≠0，解得．                8分