练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】(1) 直线kxy13k，当k变动时，所有直线都通过一个定点，求这个定点；

    (2) 过点P(1,2)作直线l交x、y轴的正半轴于A、B两点，求使取得最大值时，直线l的方程.

    【答案】(1) (3,1)；(2) xy30

    【解析】

    (1)将直线方程化为，即可得出定点坐标；

    (2)由题意可设直线方程，求出交点A，B，然后由交点都在坐标轴的正半轴可求出，然后求出，再利用均值不等式即可求出最大值，以及对应的斜率，进而求出对应的直线方程.

    解：(1)由直线方程可化为，

    则对任意的实数，且恒是直线方程的解，则可得直线恒过点(3,1)，即定点坐标为(3,1).

    (2) 由题意可知直线l的斜率存在，设直线方程为：，则, B，由交点都在坐标轴的正半轴即解得，

    又，，

    ，

    当且仅当,即时，，

    此时，直l的方程为，即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】年，在庆祝中华人民共和国成立周年之际，又迎来了以“创军人荣耀，筑世界和平”为宗旨的第七届世界军人运动会．据悉，这次军运会将于年月日至日在美丽的江城武汉举行，届时将有来自全世界多个国家和地区的近万名军人运动员参赛．相对于奥运会、亚运会等大型综合赛事，军运会或许对很多人来说还很陌生．为此，武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容，特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛，为便于对答卷进行对比研究，组委会抽取了名男生和名女生的答卷，他们的考试成绩频率分布直方图如下：

    （注：问卷满分为分，成绩的试卷为“优秀”等级）

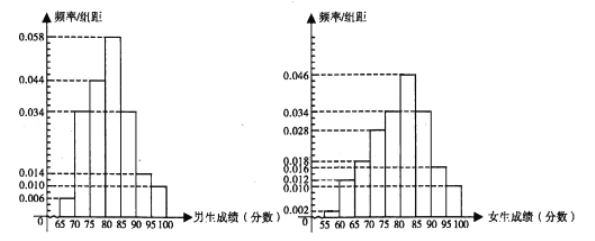
    (1)从现有名男生和名女生答卷中各取一份，分别求答卷成绩为“优秀”等级的概率；

    (2)求列联表中，，，的值，并根据列联表回答：能否在犯错误的概率不超过的前提下认为“答卷成绩为优秀等级与性别有关”？

    男

    女

    总计

    优秀

    非优秀

    总计

    (3)根据男、女生成绩频率分布直方图，对他们的成绩的优劣进行比较．

    附：参考公式：，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆与圆：有且仅有两个公共点，点、、分别是椭圆上的动点、左焦点、右焦点，三角形面积的最大值是．

    （1）求椭圆的方程；

    （2）若点在椭圆第一象限部分上运动，过点作圆的切线，过点作的垂线，求证：，交点的纵坐标的绝对值为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数.

    （Ⅰ）若，解不等式；

    （Ⅱ）当时，函数的最小值为，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等差数列的公差,前项和为,且满足,

    （1）试寻找一个等差数列和一个非负常数,使得等式对于任意的正整数恒成立,并说明你的理由；

    （2）对于（1）中的等差数列和非负常数,试求（）的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设要考察某公司生产的狂犬疫苗的剂量是否达标，现从500支疫苗中抽取50支进行检验，利用随机数表抽取样本时，先将500支疫苗按000，001，…，499进行编号，如果从随机数表第7行第8列的数开始向右读，请写出第3支疫苗的编号______________________

    （下面摘取了随机数表第7行至第9行）

    84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76

    63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79

    33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为平行四边形，已知，，于.

    （1）求证：；

    （2）若平面平面，且，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中， 与相交于点，点在线段上，，且平面．

    （1）求实数的值；

    （2）若，, 求点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一盒子中有8个大小完全相同的小球，其中3个红球，2个白球，3个黑球.

    （Ⅰ）若不放回地从盒中连续取两次球，每次取一个，求在第一次取到红球的条件下，第二次也取到红球的概率；

    （Ⅱ）若从盒中任取3个球，求取出的3个球中红球个数X的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案