
【题目】设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,起
两点,起![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)令![]() ,
, ![]() ,证明:
,证明: ![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,則第20行从左至右的第4个数字应是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①直线l的方向向量为 ![]() =(1,﹣1,2),直线m的方向向量
=(1,﹣1,2),直线m的方向向量 ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),则l与m垂直;
),则l与m垂直;
②直线l的方向向量 ![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量 ![]() =(1,﹣1,﹣1),则l⊥α;
=(1,﹣1,﹣1),则l⊥α;
③平面α、β的法向量分别为 ![]() =(0,1,3),
=(0,1,3), ![]() =(1,0,2),则α∥β;
=(1,0,2),则α∥β;
④平面α经过三点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量 ![]() =(1,u,t)是平面α的法向量,则u+t=1.
=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题的是 . (把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在长方体ABCD﹣A1B1C1D1中,E、M、N分别是BC、AE、D1C的中点,AD=AA1 , AB=2AD
(Ⅰ)证明:MN∥平面ADD1A1
(Ⅱ)求直线AD与平面DMN所成角的余弦值.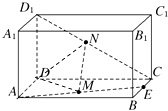
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合 ![]()
(1)求A∩B;
(2)若A∪C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
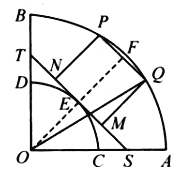
【题目】如图,已知![]() ,
, ![]() 分别是
分别是![]() 中点,弧
中点,弧![]() 的半径分别为
的半径分别为![]() ,点
,点![]() 平分弧
平分弧![]() ,过点
,过点![]() 作弧
作弧![]() 的切线分别交
的切线分别交![]() 于点
于点![]() .四边形
.四边形![]() 为矩形,其中点
为矩形,其中点![]() 在线段
在线段![]() 上,点
上,点![]() 在弧
在弧![]() 上,延长
上,延长![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)求![]() 的解析式并求其定义域;
的解析式并求其定义域;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2x|x﹣a|,其中a∈R.
(1)当a=﹣1时,在所给坐标系中作出f(x)的图象;
(2)对任意x∈[1,2],函数g(x)=﹣x+14的图象恒在函数f(x)图象的上方,求实数a的取值范围. 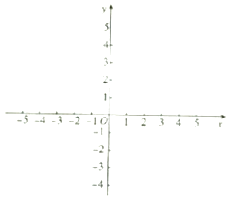
查看答案和解析>>
科目:高中数学 来源: 题型:
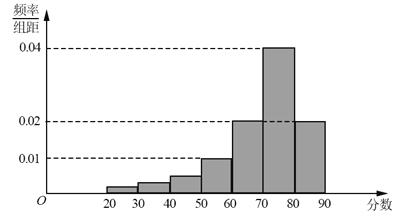
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1﹣DC﹣C1的大小为60°,则AD的长为( ) 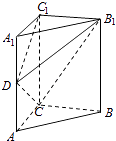
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com