
| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |
分析 根据图象求出f(x)的解析式,即可求f(x)≥log3(x+1)的解集.
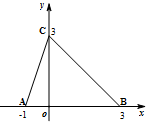
解答 解:由图象可得f(x)是分段函数,由两段直线构成.
设f(x)=kx+b,
当-1≤x≤0时,图象过(-1,0)(0,3),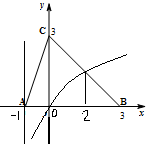
解得k=3,b=3
当0≤x≤3时,图象过(0,3)(0,3),
解得k=-1,b=3
∴f(x)=$\left\{\begin{array}{l}{3x+3,(-1≤x≤0)}\\{-x+3,(0<x≤3)}\end{array}\right.$
那么:不等式f(x)≥log3(x+1)
当-1≤x≤0时,3(x+1)≥log3(x+1),解得:x>-1
当0≤x≤3时,3-x≥log3(x+1),解得,x≤2,
对数y=log3(x+1)图象恒过(0,0),如图,数形结合法,可得答案.
综上可得:不等式f(x)≥log3(x+1)的解集为{x|-1<x≤2}.
故选B
点评 本题考查了函数的解析式的求法和对数不等式的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2}]$ | B. | (0,+∞) | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.
如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )
如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )| A. | $\frac{2\sqrt{7}}{7}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
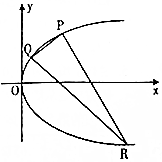 已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.
已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
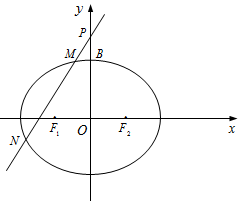 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
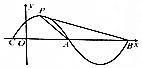 函数y=sin($\frac{π}{2}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,其中P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
函数y=sin($\frac{π}{2}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,其中P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com