
思路分析:定点到两定点的距离和为定值m,而两定点之间的距离是2,因此要分类考虑m与2的大小关系,其大小关系是我们解决问题的关键.
解:∵|PA|+|PA′|=m,|AA′|=2,|PA|+|PA′|≥|AA′|,∴m≥2.
(1)当m=2时,P点的轨迹就是线段AA′.∴其方程为y=0 (-1≤x≤1).
(2)当m>2时,由椭圆的定义知,点P的轨迹是以A、A′为焦点的椭圆.
∵2c=2,2a=m,∴a=![]() ,c=1,b2=a2-c2=
,c=1,b2=a2-c2=![]() -1
-1
.∴点P的轨迹方程为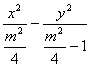 =1.
=1.
深化升华 平面内一动点到两定点的距离和等于常数时,动点的轨迹不一定是椭圆.当动点到两定点的距离和等于两定点之间的距离时,动点的轨迹是线段;当动点到两定点的距离和(常数)大于两定点之间的距离时,动点的轨迹是椭圆.


科目:高中数学 来源:设计选修数学2-1苏教版 苏教版 题型:044
若一个动点P(x,y)到两个定点F1(-1,0)、F2(3,0)的距离的差的绝对值为定值a(a≥0),试讨论点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-1苏教版 苏教版 题型:044
若一个动点P(x,y)到两个定点F1(-1,0),F2(1,0)的距离差的绝对值为定值a(a≥0)讨论点P的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com