
| A. | π | B. | $\sqrt{2}$π | C. | $\sqrt{3}$π | D. | 2π |
分析 设圆柱的高为x,则其为内接矩形的一边长,那么另一边长为y=$\sqrt{3-{x}^{2}}$,则圆柱的体积V(x)=πx(3-x2)=π(-x3+3x),0<x<$\sqrt{3}$,由此能求出该圆柱体积的最大值.
解答 解:设圆柱的高为x,则其为内接矩形的一边长,
那么另一边长为y=2$\sqrt{\frac{3}{4}-(\frac{x}{2})^{2}}$=$\sqrt{3-{x}^{2}}$,
∴圆柱的体积V(x)=πx(3-x2)=π(-x3+3x),0<x<$\sqrt{3}$,
∴V′=3π(-x2+1),
列表如下:
| x | (0,1) | 1 | (1,$\sqrt{3}$) |
| V′(x) | + | 0 | - |
点评 本题考查圆柱体体积的最大值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:填空题
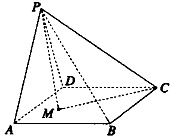 如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹的长度为$\sqrt{5}$.
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹的长度为$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
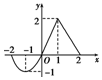 已知函数f(x)定义在[-2,2]上的图象如图所示,请分别画出下列函数的图象;
已知函数f(x)定义在[-2,2]上的图象如图所示,请分别画出下列函数的图象;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com