
【题目】已知椭圆![]() ,,过椭圆
,,过椭圆![]() 的右顶点和上顶点的直线
的右顶点和上顶点的直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点, 过点
的上顶点, 过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点, 设这两条直线的斜率分别为
两点, 设这两条直线的斜率分别为![]() ,且
,且![]() ,证明: 直线
,证明: 直线![]() 过定点
过定点
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的边长为1,弧
的边长为1,弧![]() 是以点
是以点![]() 为圆心的圆弧.
为圆心的圆弧.

(1)在正方形内任取一点![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)用大豆将正方形均匀铺满,经清点,发现大豆一共28粒,其中有22粒落在圆中阴影部分内,请据此估计圆周率![]() 的近似值(精确到
的近似值(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年五一节”期间,高速公路车辆“较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题:
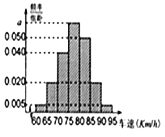
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)若该路段的车速达到或超过90km/h即视为超速行驶,求超速行驶的概率
(3)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() (
(![]() )与圆
)与圆![]() 的交点为
的交点为![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为![]() ,再由乙猜甲刚才想的数字把乙想的数字记为
,再由乙猜甲刚才想的数字把乙想的数字记为![]() ,且
,且![]() ,
, ![]() ,记
,记![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com