练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】数列{an}满足a1= ，an+1=a ﹣an+1，则M= + +…+ 的整数部分是（ ）
    A.1
    B.2
    C.3
    D.4

    【答案】A
    【解析】解：∵数列{an}满足a1= ，an+1=a ﹣an+1，

    ∴由题设知，an+1﹣1=an（an﹣1），

    ∴ = ﹣ ，

    ∴ ﹣ = ，

    通过累加，得：

    M= + +…+ =

    =2﹣ ．

    由an+1﹣an=（an﹣1）2≥0，即an+1≥an，

    由a1= ，得a2= ，∴a3=2 ．

    ∴a2018≥a2017≥a2016≥a3＞2，

    ∴0＜ ＜1，

    ∴1＜M＜2，

    ∴M的整数部分为1．

    故选：A．

    【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，B1B=B1A=AB=BC，∠B1BC=90°，D为AC的中点，AB⊥B1D．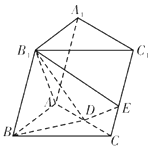
    （1）求证：平面ABB1A1⊥平面ABC；
    （2）在线段CC1（不含端点）上，是否存在点E，使得二面角E﹣B1D﹣B的余弦值为 ？若存在，求出 的值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：k2﹣8k﹣20≤0，命题q：方程 =1表示焦点在x轴上的双曲线． （Ⅰ）命题q为真命题，求实数k的取值范围；
    （Ⅱ）若命题“p∨q”为真，命题“p∧q”为假，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}，a1=1，a6=32，Sn是等差数列{bn}的前n项和，b1=3，S5=35．
    （1）求数列{an}，{bn}的通项公式；
    （2）设cn=an+bn ， 求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sinxcosx﹣sin2x﹣3cos2x+1．
    （1）求函数y=f（x）的单调递增区间；
    （2）若函数y=f（x）在区间[0，a]上恰有3个零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，给出的是计算 + + +…+ 的值的程序框图，其中判断框内可填入的是（ ）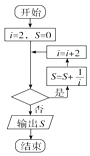
    A.i≤2 021？
    B.i≤2 019？
    C.i≤2 017？
    D.i≤2 015？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：

    分组

    频数

    频率

    [17.5，20）

    10

    0.05

    [20，225）

    50

    0.25

    [22.5，25）

    a

    b

    [25，27.5）

    40

    c

    [27.5，30]

    20

    0.10

    合计

    N

    1

    （Ⅰ）求出表中N及a，b，c的值；
    （Ⅱ）求频率分布直方图中d的值；
    （Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．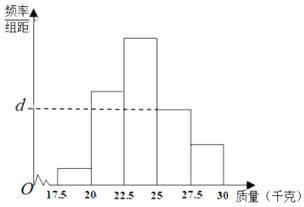

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是一个算法的流程图，则输出的a值为（ ）
    A.511
    B.1023
    C.2047
    D.4095

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（1，2）， =（cosα，sinα），设 = +t （t为实数）．
    （1）若 ，求当| |取最小值时实数t的值；
    （2）若 ⊥ ，问：是否存在实数t，使得向量 ﹣ 和向量 的夹角为 ，若存在，请求出t；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案