[题目]已知椭圆方程为 =1.其右焦点为F(4.0).过点F的直线交椭圆与A.B两点．若AB的中点坐标为.则椭圆的方程为( )A. =1B. =1C. + =1D. =1 题目和参考答案——青夏教育精英家教网—

【题目】已知椭圆方程为 =1（a＞0，b＞0），其右焦点为F（4，0），过点F的直线交椭圆与A，B两点．若AB的中点坐标为（1，﹣1），则椭圆的方程为（）
A. =1
B. =1
C. + =1
D. =1

【答案】C
【解析】解：设A（x1 ， y1），B（x2 ， y2），代入椭圆的方程可得，．两式相减可得： + =0．
由x1+x2=2，y1+y2=﹣2， = = ，代入上式可得：
=0，化为a2=3b2 ．
又c=4，c2=a2﹣b2 ，联立解得a2=24，b2=8．
∴椭圆的方程为：．
故选：C．
【考点精析】关于本题考查的椭圆的标准方程，需要了解椭圆标准方程焦点在x轴：，焦点在y轴：才能得出正确答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图所示，平面内有三个向量，，，其中与的夹角为30°，与的夹角为90°，且| |=2，| |=2，| |=2 ，若 =λ +μ ，（λ，μ∈R）则（）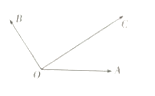
A.λ=4，μ=2
B.λ=4，μ=1
C.λ=2，μ=1
D.λ=2，μ=2

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知集合A={a|一次函数y=（4a﹣1）x+b在R上是增函数}，集合B= ．
（1）求集合A，B；
（2）设集合，求函数f（x）=x﹣ 在A∩C上的值域．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】惠城某影院共有100个座位，票价不分等次．根据该影院的经营经验，当每张标价不超过10元时，票可全部售出；当每张票价高于10元时，每提高1元，将有3张票不能售出．为了获得更好的收益，需给影院定一个合适的票价，符合的基本条件是： ①为方便找零和算帐，票价定为1元的整数倍；
②影院放映一场电影的成本费用支出为575元，票房收入必须高于成本支出．
用x（元）表示每张票价，用y（元）表示该影院放映一场的净收入（除去成本费用支出后的收入）．
（Ⅰ）把y表示成x的函数，并求其定义域；
（Ⅱ）试问在符合基本条件的前提下，每张票价定为多少元时，放映一场的净收入最多？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，正方体ABCD﹣A1B1C1D1 ，则下列四个命题：
①P在直线BC1上运动时，三棱锥A﹣D1PC的体积不变；
②P在直线BC1上运动时，直线AP与平面ACD1所成角的大小不变；
③P在直线BC1上运动时，二面角P﹣AD1﹣C的大小不变；
④M是平面A1B1C1D1上到点D和C1距离相等的点，则M点的轨迹是过D1点的直线
其中真命题的个数是（）

A.1
B.2
C.3
D.4

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】持续高温使漳州市多地出现气象干旱，城市用水紧张，为了宣传节约用水，某人准备在一片扇形区域（如图3）上按照图4的方式放置一块矩形ABCD区域宣传节约用水，其中顶点B，C在半径ON上，顶点A在半径OM上，顶点D在上，∠MON= ，ON=OM=10，m，设∠DON=θ，矩形ABCD的面积为S．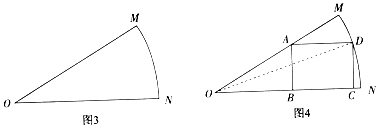
（Ⅰ）用含θ的式子表示DC，OB的长‘
（Ⅱ）若此人布置1m2的宣传区域需要花费40元，试将S表示为θ的函数，并求布置此矩形宣传栏最多要花费多少元钱？（精确到0.01）
（参考数据： ≈1.732， ≈1.414）