
分析 已知等式左边利用诱导公式化简,整理求出sinα的值,进而求出cosα的值,代入原式计算即可得到结果.
解答 解:∵sin(2π-α)=-sinα=$\frac{4}{5}$,即sinα=-$\frac{4}{5}$,α∈($\frac{3π}{2}$,2π),
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{3}{5}$,
则原式=$\frac{-\frac{4}{5}+\frac{3}{5}}{-\frac{4}{5}-\frac{3}{5}}$=$\frac{1}{7}$.
故答案为:$\frac{1}{7}$.
点评 此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1,$\frac{1}{3}$ | B. | $\frac{4}{3}$,0 | C. | $\frac{4}{3}$,-$\frac{4}{3}$ | D. | 2,2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A | B. | 2A | C. | $\frac{A}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
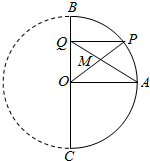 如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.
如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com