练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若x，y满足条件
    x≥y
    x+y≤1
    y≥-1
    ，则z=2x+y的最大值为（　　）
    分析：作出不等式组所表示的平面区域，由Z=2x+y可得y=-2x+z，则z为直线y=-2x+z在y轴上的截距，根据可行域判断，Z取得最大值的位置，代入可求
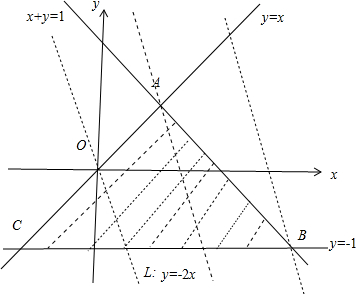
    解答：解：作出不等式组所表示的平面区域，如图所示的阴影部分的△ABC
    由Z=2x+y可得y=-2x+z，则z为直线y=-2x+z在y轴上的截距
    做直线L：2x+y=0，然后把直线L向上平移Z变大，当直线经过点B时，z最大，
    此时
    y=-1
    x+y=1
    可得B（2，-1）
    此时，zmax=3
    故选D
    点评：本题主要考查了利用线性归化的知识求解目标函数的最大值，解题的关键是判断取得最大值时的最优解的位置
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若x，y满足条件
    x+y≤3
    y≤2x
    ，则z=3x+4y的最大值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若x，y满足条件
    x≥1
    y≥1
    x+y-3≤0
    则
    2y
    x
    的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若x，y满足条件
    x+y≤3
    y≤2x
    ，则z=2x+3y的最大值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2006•南汇区二模）若x，y满足条件
    x≥0
    y≤x
    x+y≤3
    ，则2x-y的最大值是
    6
    6
    ．

    查看答案和解析>>

    同步练习册答案