
用解析法证明:等腰三角形底边延长线上一点到两腰的距离之差等于一腰上的高.
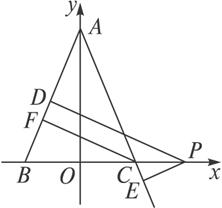
在△ABC中,AB=AC,P为BC延长线上一点,
PD⊥AB于D,PE⊥AC于E,CF⊥AB于F.
以BC所在直线为x轴,以BC中垂线为y轴,
建立直角坐标系(如图3-3-1).
设A(0,b),B(-a,0),C(a,0),(a>0,b>0),
则直线AB的方程为bx-ay+ab=0,直线AC的方程为bx+ay-ab=0,
取P(x0,0),使x0>a,
则点P到直线AB,AC的距离分别为
|PD|=![]() ,
,
|PE|=![]() .
.
点C到直线AB的距离为
|CF|=![]() ,
,
则|PD|-|PE|=![]() =|CF|.
=|CF|.
根据图形的特点,建立适当直角坐标系,利用坐标解决有关问题,这种方法叫坐标法,也称为解析法.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com