
 在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.
在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.分析 (1)延长BN,交DF于G,由已知得四边形ECFO是矩形,且EC=GF=1,从而能求出DF=2GF=2.
(2)由已知推导出BD=BF,∠DBG=∠FBG,∠CBD=∠CDB=∠ADB=45°,△BDA≌△BDN,由此能求出∠A+$\frac{1}{3}$∠ABF=135°.
解答 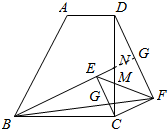 (1)解:延长BN,交DF于G,
(1)解:延长BN,交DF于G,
∵在四边形ABCD中,AD∥BC,∠ADC=90°,DC=2AD,
E为四边形ABCD内一点,F为四边形ABCD外一点,
且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N,
∴四边形ECFO是矩形,且EC=GF=1,
∵N是DC中点,且CF∥BG,
∴G是DF的中点,∴DF=2GF=2.
(2)证明:由(1)知:BG⊥DF,DG=GF,
∴BD=BF,∠DBG=∠FBG,
∵BC=CD,∴∠CBD=∠CDB=∠ADB=45°,
∵AD=DN,∠ADB=∠NDB,BD=BD,
∴△BDA≌△BDN,
∴∠ABD=∠NBD=∠FBN,
∴∠ABD=$\frac{1}{3}∠ABF$,
∵∠A+∠ABD=180°-∠ADB=135°,
∴∠A+$\frac{1}{3}$∠ABF=135°.
点评 本题考查线段长的求法,考查两角和为135°的证明,是中档题,解题时要认真审题,注意三角形全等的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | (-∞,0)∪(2,3] | C. | [0,1) | D. | (2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | $(0,\frac{1}{2}]$ | C. | $[\frac{1}{2},+∞)$ | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2(b-a) | C. | 0或2(a-b) | D. | b-a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=|x2-2x-3|.
设函数f(x)=|x2-2x-3|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com