
(本小题满分12分)
已知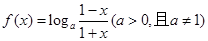
(1)求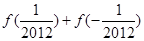 的值;
的值;
(2)当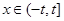 (其中
(其中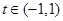 ,且
,且 为常数)时,
为常数)时,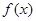 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如
果不存在,请说明理由;
(3)当 时,求满足不等式
时,求满足不等式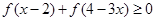 的
的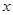 的范围.
的范围.
(1)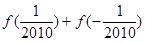 =0. (2)
=0. (2)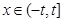 时,
时,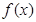 无最小值.(3)
无最小值.(3)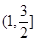
解析试题分析:(1)根据所求只要判定函数的奇偶性即可,结合定义来证明。同时对于底数a进行分类讨论得到最值。
(2)结合单调性来得到函数的不等式,进而求解取值范围。
解:(1)由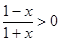 得:
得: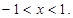 所以f(x)的定义域为:(-1,1),
所以f(x)的定义域为:(-1,1),
又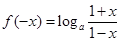
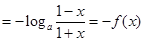 ,
,
∴f(x)为奇函数,∴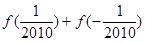 =0.
=0.
(2)设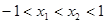 ,
,
则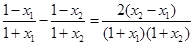
∵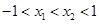 ,∴
,∴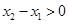 ,
,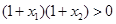 ∴
∴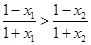 ,
,
当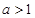 时
时
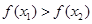 ,
,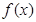 在
在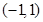 上是减函数,又
上是减函数,又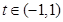
∴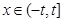 时,
时,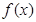 有最小值,且最小值为
有最小值,且最小值为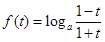
当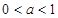 时
时
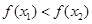 ,
,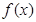 在
在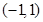 上是增函数,又
上是增函数,又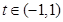
∴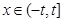 时,
时,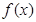 无最小值.
无最小值.
(3)由(1)及 得
得
∵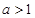 ,∴
,∴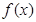 在
在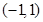 上是减函数,
上是减函数,
∴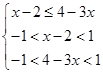 ,解得
,解得 ,∴
,∴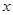 的取值范围是
的取值范围是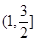
考点:本题主要考查了函数奇偶性和函数单调性的运用。
点评:解决该试题的关键是通过第一问的结构提示我们选择判定函数奇偶性,进而得到求解。同时对于底数a进行分类讨论得到函数的最值问题。


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知f (x)=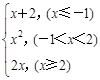 .
.
(1)求函数f (x)的值域.
(2)若f (t)=3,求t的值.
(3)用单调性定义证明在[2,+∞)上单调递增.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)已知函数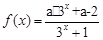 .
. 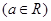
(1)是否存在实数 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;
(2)用单调性定义证明:不论 取任何实数,函数f(x)在其定义域上都是增函数;
取任何实数,函数f(x)在其定义域上都是增函数;
(3)若函数f(x)为奇函数,解不等式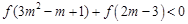 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某炮兵阵地位于地面A处,两观察所分别位于地面点C和D处, 已知CD=6000m,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.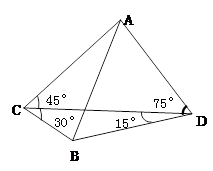
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气的含药量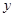 (毫克)与时间
(毫克)与时间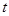 (小时)成正比.药物释放完毕后,
(小时)成正比.药物释放完毕后,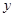 与
与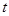 的函数关系式为
的函数关系式为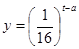 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: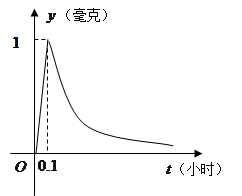
(1)求从药物释放开始,每立方米空气中的含药量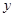 (毫克)与时间
(毫克)与时间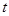 (小时)之间的函数关系式;(2)据测定,当空气中每立方米空气的含药量降到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到进教室?
(小时)之间的函数关系式;(2)据测定,当空气中每立方米空气的含药量降到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到进教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com