Question

【题目】设复数z=（x﹣1）+yi（x∈R，y≥0），若|z|≤1，则y≥x的概率为（ ）
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：∵复数z=（x﹣1）+yi（x，y∈R）且|z|≤1， ∴|z|= ≤1，即（x﹣1）2+y2≤1，
∴点（x，y）在（1，0）为圆心1为半径的圆及其内部，
而y≥x表示直线y=x左上方的部分，（图中阴影弓形）
∴所求概率为弓形的面积与圆的面积一半的之比，
∴所求概率P= = ﹣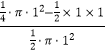
故选：C．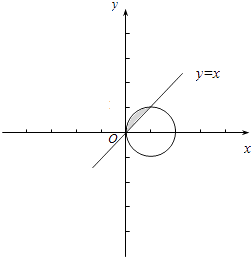

【考点精析】认真审题，首先需要了解复数的模（绝对值）(复平面内复数所对应的点到原点的距离，是非负数，因而两复数的模可以比较大小；复数模的性质：(1)(2)(3)若为虚数,则)，还要掌握几何概型(几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等)的相关知识才是答题的关键．