
分析 (Ⅰ)由题意得f1(-1)=-a1=-1,f2(-1)=-a1+a2=2,f3(-1)=-a1+a2-a3=-3,从而解得;
(Ⅱ)由fn(-1)=-a1+a2-a3+…+(-1)nan=(-1)nn,fn-1(-1)=-a1+a2-a3+…+(-1)n-1an-1=(-1)n-1(n-1),从而求通项公式;
(Ⅲ)令bn=$\frac{{a}_{n}+1}{2}$=n,从而化简S=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{nk-1}$,故2S=($\frac{1}{n}$+$\frac{1}{nk-1}$)+($\frac{1}{n+1}$+$\frac{1}{nk-2}$)+…+($\frac{1}{nk-2}$+$\frac{1}{n+1}$)+($\frac{1}{nk-1}$+$\frac{1}{n}$),结合$\frac{1}{x}$+$\frac{1}{y}$≥$\frac{4}{x+y}$可证明.
解答 解:(Ⅰ)∵f1(-1)=-a1=-1,∴a1=1,
∵f2(-1)=-a1+a2=2,∴a2=3,
∵f3(-1)=-a1+a2-a3=-3,∴a1=5;
(Ⅱ)∵fn(-1)=-a1+a2-a3+…+(-1)nan=(-1)nn,
fn-1(-1)=-a1+a2-a3+…+(-1)n-1an-1=(-1)n-1(n-1),
∴(-1)nan=(-1)nn-(-1)n-1(n-1)=(-1)n(2n-1),
∴当n≥2时,an=2n-1,且a1=1也符合an=2n-1;
故an=2n-1;
(Ⅲ)证明:令bn=$\frac{{a}_{n}+1}{2}$=n,
则S=$\frac{1}{{b}_{n}}$+$\frac{1}{{b}_{n+1}}$+$\frac{1}{{b}_{n+2}}$+…+$\frac{1}{{b}_{nk-1}}$
=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{nk-1}$,
故2S=($\frac{1}{n}$+$\frac{1}{nk-1}$)+($\frac{1}{n+1}$+$\frac{1}{nk-2}$)+…+($\frac{1}{nk-2}$+$\frac{1}{n+1}$)+($\frac{1}{nk-1}$+$\frac{1}{n}$),
∵当x>0,y>0时,$\frac{1}{x}$+$\frac{1}{y}$-$\frac{4}{x+y}$=$\frac{(x-y)^{2}}{xy(x+y)}$≥0,
∴$\frac{1}{x}$+$\frac{1}{y}$≥$\frac{4}{x+y}$,
故2S>$\frac{4}{n+nk-1}$+$\frac{4}{n+1+nk-2}$+…+$\frac{4}{n+nk-1}$=$\frac{4n(k-1)}{n+nk-1}$,
故S>$\frac{2(k-1)}{1+k-\frac{1}{n}}$>$\frac{2(k-1)}{k+1}$=2(1-$\frac{2}{k+1}$)>2(1-$\frac{2}{7+1}$)=$\frac{3}{2}$;
故当k>7且k∈N*时,对任意n∈N*都有$\frac{2}{{{a_n}+1}}+\frac{2}{{{a_{n+1}}+1}}+\frac{2}{{{a_{n+2}}+1}}+…+\frac{2}{{{a_{nk-1}}+1}}>\frac{3}{2}$成立.
点评 本题考查了等差数列的通项公式的求法及放缩法的应用,关键在于不等式$\frac{1}{x}$+$\frac{1}{y}$≥$\frac{4}{x+y}$的判断与应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
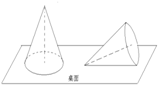 用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
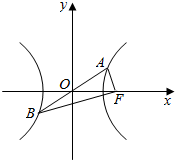 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为是双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,α∈[$\frac{π}{12}$,$\frac{π}{6}$],则该双曲线离心率e的取值范围为[$\sqrt{2}$,$\sqrt{3}$+1].
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为是双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,α∈[$\frac{π}{12}$,$\frac{π}{6}$],则该双曲线离心率e的取值范围为[$\sqrt{2}$,$\sqrt{3}$+1].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,-\frac{{\sqrt{6}}}{6}),(0,\frac{{\sqrt{6}}}{6})$ | B. | $(-\frac{{\sqrt{6}}}{6},0),(\frac{{\sqrt{6}}}{6},0)$ | C. | (-1,0),(1,0) | D. | (0,-1)、(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com