
【题目】设函数f(x)=ln(x﹣1)+ax2+x+1,g(x)=(x﹣1)ex+ax2 , a∈R. (Ⅰ)当a=1时,求函数f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若函数g(x)有两个零点,试求a的取值范围;
(Ⅲ)证明f(x)≤g(x)
【答案】解:(Ⅰ)函数f(x)的定义域是(1,+∞), ![]() . 当a=1时,f'(2)=4a+2=6,f(2)=4a+3=7.
. 当a=1时,f'(2)=4a+2=6,f(2)=4a+3=7.
所以函数f(x)在点(2,f(2))处的切线方程为y﹣7=6(x﹣2).
即y=6x﹣5
(Ⅱ)函数g(x)的定义域为R,由已知得g'(x)=x(ex+2a).
①当a=0时,函数g(x)=(x﹣1)ex只有一个零点;
②当a>0,因为ex+2a>0,
当x∈(﹣∞,0)时,g'(x)<0;当x∈(0,+∞)时,g'(x)>0.
所以函数g(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增.
又g(0)=﹣1,g(1)=a,
因为x<0,所以x﹣1<0,ex<1,所以ex(x﹣1)>x﹣1,所以g(x)>ax2+x﹣1
取 ![]() ,显然x0<0且g(x0)>0
,显然x0<0且g(x0)>0
所以g(0)g(1)<0,g(x0)g(0)<0.
由零点存在性定理及函数的单调性知,函数有两个零点.
③当a<0时,由g'(x)=x(ex+2a)=0,得x=0,或x=ln(﹣2a).
ⅰ) 当 ![]() ,则ln(﹣2a)>0.
,则ln(﹣2a)>0.
当x变化时,g'(x),g(x)变化情况如下表:
x | (﹣∞,0) | 0 | (0,ln(﹣2a)) | ln(﹣2a) | (ln(﹣2a),+∞) |
g'(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↗ | ﹣1 | ↘ | ↗ |
注意到g(0)=﹣1,所以函数g(x)至多有一个零点,不符合题意.
ⅱ) 当 ![]() ,则ln(﹣2a)=0,g(x)在(﹣∞,+∞)单调递增,函数g(x)至多有一个零点,不符合题意.
,则ln(﹣2a)=0,g(x)在(﹣∞,+∞)单调递增,函数g(x)至多有一个零点,不符合题意.
若 ![]() ,则ln(﹣2a)≤0.
,则ln(﹣2a)≤0.
当x变化时,g'(x),g(x)变化情况如下表:
x | (﹣∞,ln(﹣2a)) | ln(﹣2a) | (ln(﹣2a),0) | 0 | (0,+∞) |
g'(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↗ | ↘ | ﹣1 | ↗ |
注意到当x<0,a<0时,g(x)=(x﹣1)ex+ax2<0,g(0)=﹣1,所以函数g(x)至多有一个零点,不符合题意.
综上,a的取值范围是(0,+∞).
(Ⅲ)证明:g(x)﹣f(x)=(x﹣1)ex﹣ln(x﹣1)﹣x﹣1.
设h(x)=(x﹣1)ex﹣ln(x﹣1)﹣x﹣1,其定义域为(1,+∞),则证明h(x)≥0即可.
因为 ![]() ,取
,取 ![]() ,则
,则 ![]() ,且h'(2)>0.
,且h'(2)>0.
又因为 ![]() ,所以函数h'(x)在(1,+∞)上单增.
,所以函数h'(x)在(1,+∞)上单增.
所以h'(x)=0有唯一的实根x0∈(1,2),且 ![]() .
.
当1<x<x0时,h'(x)<0;当x>x0时,h'(x)>0.
所以函数h(x)的最小值为h(x0).
所以 ![]() =1+x0﹣x0﹣1=0.
=1+x0﹣x0﹣1=0.
所以f(x)≤g(x).
【解析】(Ⅰ)求出函数的导数,计算f(2),f′(2)的值,求出切线方程即可;(Ⅱ)求出函数g(x)的导数,通过讨论a的范围,判断函数g(x)的单调性结合函数零点的个数确定a的范围即可;(Ⅲ)设h(x)=(x﹣1)ex﹣ln(x﹣1)﹣x﹣1,其定义域为(1,+∞),只需证明h(x)≥0即可,根据函数的单调性求出h(x)的最小值,从而证出结论.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知左、右焦点分别为F1(﹣c,0),F2(c,0)的椭圆 ![]() 过点
过点 ![]() ,且椭圆C关于直线x=c对称的图形过坐标原点.
,且椭圆C关于直线x=c对称的图形过坐标原点.
(I)求椭圆C的离心率和标准方程.
(II)圆 ![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆P1的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆P1的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级” (Ⅰ)求乙班总分超过甲班的概率
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分
①请你从平均分光和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为ξ,求ξ的分布列及数学期望.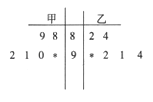
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,等腰梯形BCDP中,BC∥PD,BA⊥PD于点A,PD=3BC,且AB=BC=1.沿AB把△PAB折起到△P'AB的位置(如图2),使∠P'AD=90°. (Ⅰ)求证:CD⊥平面P'AC;
(Ⅱ)求二面角A﹣P'D﹣C的余弦值;
(Ⅲ)线段P'A上是否存在点M,使得BM∥平面P'CD.若存在,指出点M的位置并证明;若不存在,请说明理由.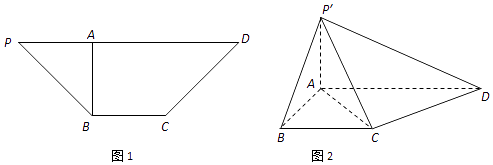
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合M满足:x,y∈M,都有x+y∈M,xy∈M,则称集合M是封闭的.显然,整数集Z,有理数集Q都是封闭的.对于封闭的集合M(MR),f:M→M是从集合到集合的一个函数, ①如果都有f(x+y)=f(x)+f(y),就称是保加法的;
②如果x,y∈M都有f(xy)=f(x)f(y),就称f是保乘法的;
③如果f既是保加法的,又是保乘法的,就称f在M上是保运算的.
在上述定义下,集合 ![]() 封闭的(填“是”或“否”);若函数f(x)在Q上保运算,并且是不恒为零的函数,请写出满足条件的一个函数f(x)= .
封闭的(填“是”或“否”);若函数f(x)在Q上保运算,并且是不恒为零的函数,请写出满足条件的一个函数f(x)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=﹣x0 , 则称x0是f(x)的一个“次不动点”,也称f(x)在区间D上存在次不动点.若函数f(x)=ax2﹣3x﹣a+ ![]() 在区间[1,4]上存在次不动点,则实数a的取值范围是( )
在区间[1,4]上存在次不动点,则实数a的取值范围是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(Ⅱ)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π.若将函数f(x)的图象向左平移 ![]() 个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
A.f(x)=2sin(x+ ![]() )
)
B.f(x)=2sin(x+ ![]() )?
)?
C.f(x)=2sin(2x+ ![]() )
)
D.f(x)=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x+1(a∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对任意x∈(0,+∞),都有f(x)≤0,求实数a的取值范围;
(Ⅲ)证明 ![]() (其中n∈N* , e为自然对数的底数).
(其中n∈N* , e为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com