
【题目】已知![]() (
(![]() ),下列结论正确的是( )
),下列结论正确的是( )
①当![]() 时,
时,![]() 恒成立;②当
恒成立;②当![]() 时,
时,![]() 的零点为
的零点为![]() 且
且![]() ;③当
;③当![]() 时,
时,![]() 是
是![]() 的极值点;④若
的极值点;④若![]() 有三个零点,则实数k的取值范围为
有三个零点,则实数k的取值范围为![]() .
.
A.①②④B.①③C.②③④D.②④
【答案】D
【解析】
①当![]() 时,当
时,当![]() 时,
时,![]() ,即可判断真假;②当
,即可判断真假;②当![]() 时,求导求出
时,求导求出![]() 的单调区间,再结合零点存在性定理,判断
的单调区间,再结合零点存在性定理,判断![]() 是否异号;③当
是否异号;③当![]() 时,求导,求出单调区间,即可判断真假;④令
时,求导,求出单调区间,即可判断真假;④令![]() 分离参数,转化为求
分离参数,转化为求![]() 有三个交点时,
有三个交点时,![]() 的范围,通过求导研究函数
的范围,通过求导研究函数![]() 的图像,即可求出结论.
的图像,即可求出结论.
当![]() 时,
时,![]() ,
,![]() ,故①错误;
,故①错误;
当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,故
,故![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,
,![]() ,
,
由函数零点存在性定理知,存在![]() ,使得
,使得![]() ,故②正确;
,故②正确;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
令![]() ,
,![]() ,令
,令![]() ,
,
解得![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 不是
不是![]() 的极值点,故③错误;
的极值点,故③错误;
![]() 有三个零点等价于方程
有三个零点等价于方程![]() 有三个根,
有三个根,
即方程![]() 有三个根,
有三个根,
令![]() ,
,![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
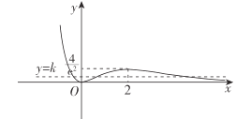
大致图象如图所示,故k的取值范围为![]() ,④正确.
,④正确.
故选:D.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +
+![]() .
.
(1)当m=0时,求不等式f(x)≤9的解集;
(2)当m=2时,若x∈(1,4),f(x) ![]() 2x
2x![]() a<0,求a的取值范围.
a<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求
上为单调函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,试判断方程
时,试判断方程![]() 是否有实数解,并说明理由.
是否有实数解,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为自然对数的底数) .
为自然对数的底数) .
(1)若![]() 在
在![]() 处的取得极值为1,求
处的取得极值为1,求![]() 及
及![]() 的值;
的值;
(2)![]() 时,讨论函数
时,讨论函数![]() 的极值;
的极值;
(3)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cos θ,直线l的参数方程为![]() (t为参数,α为直线的倾斜角).
(t为参数,α为直线的倾斜角).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C有唯一的公共点,求角α的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个棱锥的底面是正方形,且顶点在底面内的射影是底面的中心,那么这样的棱锥叫正四棱锥.若一正四棱锥的体积为18,则该正四棱锥的侧面积最小时,以下结论正确的是( ).
A.棱的高与底边长的比为![]() B.侧棱与底面所成的角为
B.侧棱与底面所成的角为![]()
C.棱锥的高与底面边长的比为![]() D.侧棱与底面所成的角为
D.侧棱与底面所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

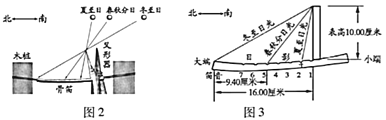
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为3,实轴长为1的双曲线![]() (
(![]() )的左焦点为
)的左焦点为![]() ,顶点在原点的抛物线
,顶点在原点的抛物线![]() 的准线经过点
的准线经过点![]() ,且抛物线
,且抛物线![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,且满足
,且满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com