
【题目】已知函数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的最大、最小值;
上的最大、最小值;
(2)求证:在区间![]() 上,函数
上,函数![]() 的图象在函数
的图象在函数![]() 的图象的下方.
的图象的下方.
【答案】(1)由已知![]() ,
,
当![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以函数![]() 在区间
在区间![]() 上的最大、最小值分别为
上的最大、最小值分别为![]() ,
,![]() ,
,
所以函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
(2)证明:设![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
又![]() ,所以在区间
,所以在区间![]() 上,
上,![]() ,即
,即![]() ,
,
所以在区间![]() 上函数
上函数![]() 的图象在函数
的图象在函数![]() 图象的下方.
图象的下方.
【解析】
(1)求得函数的导数![]() ,得到函数的单调性,进而求解函数的最值;
,得到函数的单调性,进而求解函数的最值;
(2)由题意,设![]() ,求得
,求得![]() ,利用导数求得函数的单调性和最小值,即作出证明.
,利用导数求得函数的单调性和最小值,即作出证明.
解:(1)由f(x)=![]() x2+ln x有f′(x)=x+
x2+ln x有f′(x)=x+![]() ,
,
当x∈[1,e]时,f′(x)>0,
所以f(x)max=f(e)=![]() e2+1.
e2+1.
f(x)min=f(1)=![]() .
.
(2)设F(x)=![]() x2+ln x-
x2+ln x-![]() x3,
x3,
则F′(x)=x+![]() -2x2=
-2x2=![]() ,
,
当x∈[1,+∞)时,F′(x)<0,
且F(1)=-![]() <0故x∈[1,+∞)时F(x)<0,
<0故x∈[1,+∞)时F(x)<0,
所以![]() x2+ln x<
x2+ln x<![]() x3,得证.
x3,得证.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,定义域为[0,2π],g(x) 为f(x) 的导函数.
,定义域为[0,2π],g(x) 为f(x) 的导函数.
(1)求方程g(x)=0 的解集;
(2)求函数g(x) 的最大值与最小值;
(3)若函数F(x)=f(x)﹣ax 在定义域上恰有2个极值点,求实数a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用![]() 表示.
表示.
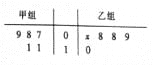
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣5:不等式选讲
设函数f(x)=|2x﹣4|+|x+2|
(1)求函数y=f(x)的最小值;
(2)若不等式f(x)≥|a+4|﹣|a﹣3|恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:m∈R,且m+1≤0,q:x∈R,x2+mx+1>0恒成立,若p∧q为假命题且p∨q为真命题,则m的取值范围是__________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a、b、c,已知向量 ![]() =(cosA,cosB),
=(cosA,cosB), ![]() =(a,2c﹣b),且
=(a,2c﹣b),且 ![]() ∥
∥ ![]() .
.
(1)求角A的大小;
(2)若a=4,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ax2+bx,(a,b∈R).
(1)设a=1,f(x)在x=1处的切线过点(2,6),求b的值;
(2)设b=a2+2,求函数f(x)在区间[1,4]上的最大值;
(3)定义:一般的,设函数g(x)的定义域为D,若存在x0∈D,使g(x0)=x0成立,则称x0为函数g(x)的不动点.设a>0,试问当函数f(x)有两个不同的不动点时,这两个不动点能否同时也是函数f(x)的极值点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com