[题目]设复数z＝2m+(4-m2)i.当实数m取何值时.复数z对应的点:(1)位于虚轴上?(2)位于一.三象限?(3)位于以原点为圆心.以4为半径的圆上? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设复数z＝2m＋(4－m2)i，当实数m取何值时，复数z对应的点：

(1)位于虚轴上？

(2)位于一、三象限？

(3)位于以原点为圆心，以4为半径的圆上？

【答案】(1)m＝0 (2)m＜－2或0＜m＜2 (3)m＝0或m＝±2

【解析】(1)复数z对应的点位于虚轴上，则

m＝0.

∴m＝0时，复数z对应的点位于虚轴上．

(2)复数z对应的点位于一、三象限，则

2m·(4－m2)＞0m(m－2)(m＋2)＜0m＜－2或0＜m＜2.

∴m＜－2或0＜m＜2时，复数z对应的点位于一、三象限．

(3)复数z对应的点位于以原点为圆心，以4为半径的圆上，则|z|＝＝4m＝0或m＝±2.

∴m＝0或m＝±2时，复数z对应的点位于以原点为圆心，以4为半径的圆上．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知圆N经过点A（3，1），B（﹣1，3），且它的圆心在直线3x﹣y﹣2=0上．

（1）求圆N的方程；

（2）若点D为圆N上任意一点，且点C（3，0），求线段CD的中点M的轨迹方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在如图所示的圆锥中，OP是圆锥的高，AB是底面圆的直径，点C是弧AB的中点，E是线段AC的中点，D是线段PB的中点，且PO=2,OB=1．

（1）试在PB上确定一点F，使得EF∥面COD，并说明理由；

（2）求点到面COD的距离．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD中，△PAB是正三角形，四边形ABCD是矩形，且平面PAB⊥平面ABCD，PA=2，PC=4．

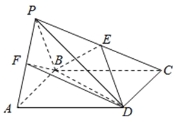
（Ⅰ）若点E是PC的中点，求证：PA∥平面BDE；

（Ⅱ）若点F在线段PA上，且FA=λPA，当三棱锥B﹣AFD的体积为时，求实数λ的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入万元广告费用，并将各地的销售收益绘制成频率分布直方图（如图所示）.由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从开始计数的.

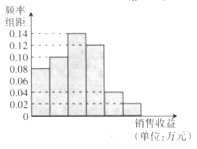
（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度；

（Ⅱ）估计该公司投入万元广告费用之后，对应销售收益的平均值（以各组的区间中点值代表该组的取值）；

（Ⅲ）该公司按照类似的研究方法，测得另外一些数据，并整理得到下表：

广告投入x（单位：万元）	1	2	3	4	5
销售收益y（单位：万元）	2	3	2		7

表中的数据显示，与之间存在线性相关关系，请将（Ⅱ）的结果填入空白栏，并计算关于的回归方程.

回归直线的斜率和截距的最小二乘估计公式分别为.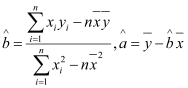

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知甲、乙两煤矿每年的产量分别为200万吨和300万吨，需经过东车站和西车站两个车站运往外地，东车站每年最多能运280万吨煤，西车站每年最多能运360万吨煤，甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨，乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨．要使总运费最少，煤矿应怎样编制调运方案？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=，其中0<a<1，k∈Ｒ。