
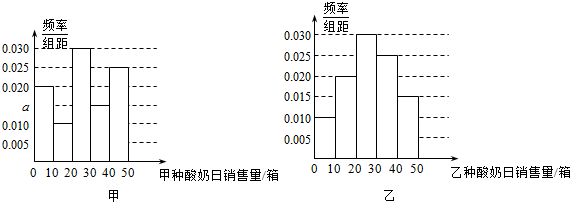
分析 (Ⅰ)由各小矩形面积和为1,先求出a,由频率分布直方图可看出,甲的销售量比较分散,而乙较为集中,由此能比s12,s22的大小.
(Ⅱ)由题意可知X的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望EX.
解答 解:(Ⅰ)由各小矩形面积和为1,
得(0.010+a+0.020+0.025+0.030)×10=1,
解得a=0.015,
由频率分布直方图可看出,甲的销售量比较分散,而乙较为集中,主要集中在20-30箱,
故s12>s22.
(Ⅱ)由题意可知X的所有可能取值为0,1,2,3,
P(X=0)=${C}_{3}^{0}×0.{3}^{0}×0.{7}^{3}$=0.343,
P(X=1)=${C}_{3}^{1}×0.3×0.{7}^{2}$=0.441,
P(X=2)=${C}_{3}^{2}×0.{3}^{2}×0.7$=0.189,
P(X=3)=${C}_{3}^{3}×0.{3}^{3}×0.{7}^{0}$=0.027,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评 本题考查频率分布直方图的性质的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-1-\frac{{\sqrt{2}}}{2}$ | B. | -1 | C. | 0 | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
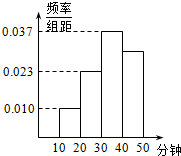 某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在40~50分钟的人数为81.
某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在40~50分钟的人数为81.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com