
【题目】在直角坐标系xOy 中,F,A,B 分别为椭圆 ![]() 的右焦点、右顶点和上顶点,若
的右焦点、右顶点和上顶点,若 ![]()
(1)求a的值;
(2)过点P(0,2)作直线l 交椭圆于M,N 两点,过M 作平行于x 轴的直线交椭圆于另外一点Q,连接NQ ,求证:直线NQ 经过一个定点.
【答案】
(1)解:由题意得: 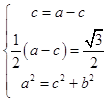 ,解得
,解得 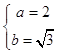 ,
,
∴a的值为2;
(2)解:设M(x1,y1),N(x2,y2),直线l 的方程为y=kx+2,
则Q(﹣x1,y1),
将y=kx+2 代入椭圆方程得(3+4k2)x2+16kx+4=0,
![]() ,
,
直线NQ 的方程 ![]() ,
,
由对称性可知,若过定点,则必在y 轴上,
令x=0,得 ![]() ,
, ![]() ,
,
所以直线NQ 经过定点(0, ![]() ).
).
【解析】(1)由题意得: 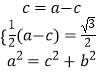 ,解得a;(2)设M(x1,y1),N(x2,y2),直线l 的方程为y=kx+2,将y=kx+2 代入椭圆方程得(3+4k2)x2+16kx+4=0,
,解得a;(2)设M(x1,y1),N(x2,y2),直线l 的方程为y=kx+2,将y=kx+2 代入椭圆方程得(3+4k2)x2+16kx+4=0, ![]() ,直线NQ 的方程
,直线NQ 的方程 ![]() ,由对称性可知,若过定点,则必在y 轴上,令x=0,即可.
,由对称性可知,若过定点,则必在y 轴上,令x=0,即可.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+bx2+cx(x∈R),已知g(x)=f(x)﹣f′(x)是奇函数.
(Ⅰ)求b,c的值.
(Ⅱ)求g(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1(b>0)的左、右焦点分别为F1、F2 , 点F2也为抛物线C2:y2=8x的焦点,过点F2的直线l交抛物线C2于A,B两点.
=1(b>0)的左、右焦点分别为F1、F2 , 点F2也为抛物线C2:y2=8x的焦点,过点F2的直线l交抛物线C2于A,B两点.
(Ⅰ)若点P(8,0)满足|PA|=|PB|,求直线l的方程;
(Ⅱ)T为直线x=﹣3上任意一点,过点F1作TF1的垂线交椭圆C1于M,N两点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30 ![]() nmile,CD=250
nmile,CD=250 ![]() nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ= .
nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ= . 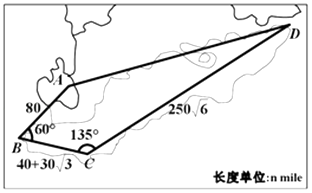
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为偶函数,当x<0时,f(x)=ln(﹣x)﹣ax.若直线y=x与曲线y=f(x)至少有两个交点,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 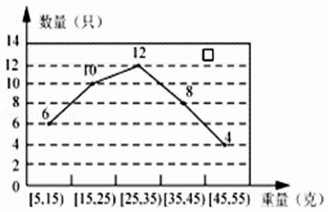
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别是a、b、c,已知sinB+sinC=msinA(m∈R),且a2﹣4bc=0.
(1)当a=2, ![]() 时,求b、c的值;
时,求b、c的值;
(2)若角A为锐角,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com