
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面积等于![]() ,求ab的最小值.
,求ab的最小值.
【答案】(1)C![]() ;(2)最小值为
;(2)最小值为![]()
【解析】
(1)由正弦定理![]() ,将2ccosB=2a+b变形为2sinCcosB=2sin(B+C)+sinB,使用两角和的正弦公式化简等式即可求得C的值;
,将2ccosB=2a+b变形为2sinCcosB=2sin(B+C)+sinB,使用两角和的正弦公式化简等式即可求得C的值;
(2)由△ABC的面积公式得出c与a、b的关系为c=3ab,将其代入余弦定理,并通过基本不等式进行变形,可求得ab的最小值.
(1)由正弦定理可知:![]() 2R,
2R,
a=2RsinA,b=2RsinB,c=2RsinC,其中R为△ABC的外接圆半径,
由2ccosB=2a+b,则2sinCcosB=2sin(B+C)+sinB,可得:2sinBcosC+sinB=0,
由0<B<π,sinB≠0,cosC![]() ,0<C<π,则C
,0<C<π,则C![]() ;
;
(2)由S![]() absinC
absinC![]() ab
ab![]() ,则c=3ab,又c2=a2+b2﹣2abcosC=a2+b2+ab,
,则c=3ab,又c2=a2+b2﹣2abcosC=a2+b2+ab,
由a2+b2≥2ab,当且仅当a=b时取等号,可得:2ab+ab≤9a2b2,即ab![]() ,
,
则当a=b时,ab取得的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,数列
,数列![]() 为
为![]() 数列,记
数列,记![]() .
.
(1)写出一个满足![]() ,且
,且![]() 的
的![]() 数列
数列![]() ;
;
(2)若![]() ,
,![]() ,证明:
,证明:![]() 数列
数列![]() 是递增数列的充要条件是
是递增数列的充要条件是![]() ;
;
(3)对任意给定的整数![]() ,是否存在首项为0的
,是否存在首项为0的![]() 数列
数列![]() ,使得
,使得![]() ?如果存在,写出一个满足条件的
?如果存在,写出一个满足条件的![]() 数列
数列![]() ;如果不存在,说明理由.
;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是我国古代计算圆周率![]() 的一种方法.在公元
的一种方法.在公元![]() 年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求
年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求![]() .当时刘微就是利用这种方法,把
.当时刘微就是利用这种方法,把![]() 的近似值计算到
的近似值计算到![]() 和
和![]() 之间,这是当时世界上对圆周率
之间,这是当时世界上对圆周率![]() 的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率
的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率![]() ,则
,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() )(参考数据
)(参考数据![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某语文报社为研究学生课外阅读时间与语文考试中的作文分数的关系,随机调查了本市某中学高三文科班![]() 名学生每周课外阅读时间
名学生每周课外阅读时间![]() (单位:小时)与高三下学期期末考试中语文作文分数
(单位:小时)与高三下学期期末考试中语文作文分数![]() ,数据如下表:
,数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 38 | 40 | 43 | 45 | 50 | 54 |
(1)根据上述数据,求出高三学生语文作文分数![]() 与该学生每周课外阅读时间
与该学生每周课外阅读时间![]() 的线性回归方程,并预测某学生每周课外阅读时间为
的线性回归方程,并预测某学生每周课外阅读时间为![]() 小时时其语文作文成绩;
小时时其语文作文成绩;
(2)从这![]() 人中任选
人中任选![]() 人,这
人,这![]() 人中至少有
人中至少有![]() 人课外阅读时间不低于
人课外阅读时间不低于![]() 小时的概率.
小时的概率.
参考公式:![]() ,其中
,其中 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地中小学生的近视形成原因,教育部门委托医疗机构对该地所有中小学生的视力做了一次普查.现该地中小学生人数和普查得到的近视情况分别如图1和图2所示.
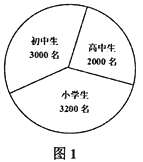
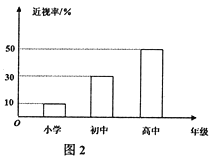
(1)求该地中小学生的平均近视率(保留两位有效数字);
(2)为调查中学生用眼卫生习惯,该地用分层抽样的方法从所有初中生和高中生中确定5人进行问卷调查,再从这5人中随机选取2人继续访谈,则此2人全部来自高中年级的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
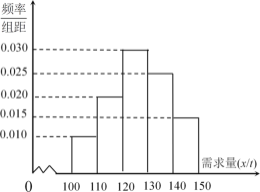
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com