
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
,![]() 分别交
分别交![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 的准线于
的准线于![]() ,
,![]() 两点.
两点.
(1)若![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,证明:
的中点,证明:![]() ;
;
(2)若△![]() 的面积是△
的面积是△![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
科目:高中数学 来源: 题型:
【题目】设命题P;实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0
(1)若a=1,且![]() 为真命题,求实数x的取值范围。
为真命题,求实数x的取值范围。
(2)若p是q成立的必要不充分条件,求实数a 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,学校举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确给改选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() 的概率;
的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下![]() 组:第1组
组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求a的值;
(Ⅱ)现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生座谈,求每组抽取的学生人数;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计随机抽取学生所得测试分数的平均值在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 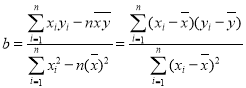 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() 对任意实数
对任意实数![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线.
轴上的双曲线.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题:“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com