
【题目】如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点 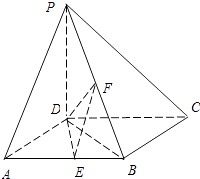
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(3)求DB与平面DEF所成角的正弦值.
【答案】
(1)证明:以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),
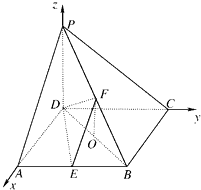
设AD=a,则D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、E(a, ![]() ,0)、F(
,0)、F( ![]() ,
, ![]() ,
, ![]() )、P(0,0,a)
)、P(0,0,a)
∵ ![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() ),
), ![]() =(0,a,0),
=(0,a,0),
∴ ![]()
![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() )(0,a,0)=0,
)(0,a,0)=0,
∴ ![]() ⊥
⊥ ![]()
∴EF⊥DC
(2)解:设G(x,0,z),则G∈平面PAD.
![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ,z﹣
,z﹣ ![]() ),
),
![]()
![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ,z﹣
,z﹣ ![]() )(a,0,0)=a(x﹣
)(a,0,0)=a(x﹣ ![]() )=0,∴x=
)=0,∴x= ![]() ;
;
![]()
![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ,z﹣
,z﹣ ![]() )(0,﹣a,a)=
)(0,﹣a,a)= ![]() +a(z﹣
+a(z﹣ ![]() )=0,∴z=0.
)=0,∴z=0.
∴G点坐标为( ![]() ,0,0),即G点为AD的中点
,0,0),即G点为AD的中点
(3)解:设平面DEF的法向量为 ![]() =(x,y,z).
=(x,y,z).
由 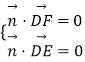 得:
得: 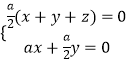
取x=1,则y=﹣2,z=1,
∴ ![]() =(1,﹣2,1).
=(1,﹣2,1).
cos< ![]() ,
, ![]() >=
>= 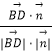 =
= ![]() =
= ![]() ,
,
∴DB与平面DEF所成角的正弦值的大小为 ![]()
【解析】以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,设AD=a,可求出各点的坐标;(1)求出EF和CD的方向向量,根据向量垂直的充要条件,可证得 ![]() ⊥
⊥ ![]() ,即EF⊥DC.(2)设G(x,0,z),根据线面垂直的性质,可得
,即EF⊥DC.(2)设G(x,0,z),根据线面垂直的性质,可得 ![]()
![]() =
= ![]()
![]() =0,进而可求出x,z值,得到G点的位置;(3)求出平面DEF的法向量为
=0,进而可求出x,z值,得到G点的位置;(3)求出平面DEF的法向量为 ![]() ,及DB的方向
,及DB的方向 ![]() 的坐标,代入向量夹角公式,可得DB与平面DEF所成角的正弦值
的坐标,代入向量夹角公式,可得DB与平面DEF所成角的正弦值
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想,以及对直线与平面垂直的性质的理解,了解垂直于同一个平面的两条直线平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设p:A={x|2x2﹣3ax+a2<0},q:B={x|x2+3x﹣10≤0}.
(1)求A;
(2)当a<0时,若¬p是¬q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为![]() 中位数分别为
中位数分别为![]() 则( )
则( )

A. x甲<x乙,m甲>m乙 B. x甲>x乙,m甲>m乙
C. x甲>x乙,m甲<m乙 D. x甲<x乙,m甲<m乙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某几何体的三视图都是直角三角形,则该几何体的体积等于__________.
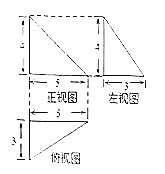
【答案】10
【解析】几何体为三棱锥,(高为4,底面为直角三角形),体积为![]()
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.
(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.
【题型】填空题
【结束】
15
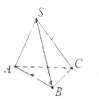
【题目】如图:在三棱锥![]() 中,已知底面
中,已知底面![]() 是以
是以![]() 为斜边的等腰直角三角形,且侧棱长
为斜边的等腰直角三角形,且侧棱长![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积等于__________.
的外接球的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com